Пару различных простых чисел, между которыми нет других простых чисел, можно называть последовательными или соседними.
И про пары соседних простых чисел доказано некоторое количество теорем (это и все последующее я пишу для
Altenter). Например, доказано, что для любого натурального

найдется отрезок из

подряд идущих составных чисел. Упражнение для
Altenter: попробуйте это доказать, тут не требуется ничего сложнее факториала (и это уже жирнющая подсказка). А есть гораздо более нетривиальная теорема Эрдёша и Турана, я бы даже не пытался сам ее доказывать. Пусть

– последовательность всех простых чисел в порядке возрастания,
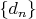
– последовательность разностей соседних простых чисел:
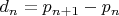
. Теорема: не существует

, начиная с которого последовательность
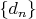
строго монотонна.
У меня мозг работает по- другому - не приспособлен к системному обучению. Испортил в детстве его чтением романов, фантастики, приключений, детективов научпопа и т.д. Учебники читаю со скоростью приключенческого романа. Но вот только когда читаю рассказ возникают образы, погружение в обстановку, переживание, а когда читаю учебник - пробегают перед глазами значки, буквы, слова, предложения и ни смыслов, ни образов не возникает. Скука-скучная и хочется плакать и спать. Зато когда начинаешь фантазировать про математику, тогда возникает образ, начинаешь его сопоставлять и исследовать, и погружаться в обстановку, и испытывать эффект присутствия, и когда обсуждаешь это и пытаешься сопоставить с тем, что уже известно, понимаешь, что что-то понимаешь, тогда вот это становится интересным и увлекательным.
А зачем вообще ввели в терминологию "простых близнецов"?
Затем, что о них можно поставить содержательные математические задачи. Например, если Вы докажете или опровергните, что множество всех пар близнецов конечно, Вы войдете в историю математики. А есть еще пары кузенов - это простые числа, отличающиеся на четверку, например, 7 и 11, 13 и 17. Неизвестно, конечно ли множество всех пар кузенов, и это отдельная проблема, которая не сводится к проблеме близнецов (по крайней мере, насколько сейчас известно). Если Вы решите эту проблему, Вы тоже войдете в историю. Да, таких вопросов можно поставить много. Например, только в 2013 г. было
доказано: существует бесконечное множество таких пар различных простых чисел

, что
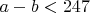
. Был ли с тех пор улучшен этот результат, я не знаю.
А если что-либо из этого докажете Вы, то Вы войдете в историю математики)))
Я понял, вы любите когда все разложено по полочкам, шкафчикам строго на своих местах и ничего не смешивается, иначе Вам трудно и это напрягает )
Как бы сказать повежливее. Уважаемый
Someone - профессиональный и опытный математик. Он знает, какие "полочки и шкафчики" нужны, чтобы продуктивно заниматься математикой. Мне, например, у него учиться и учиться.
Конечно
Someone и уважаемый, и профессиональный, и опытный, и математик. И если Вам у него учиться и учиться, то мне сначала надо учиться у Вас, а потом, может быть, когда-нибудь, если повезет, у него. Но это же путь в никуда. Поэтому, чтобы не идти в никуда, а хотя бы оставаться на месте, то учась у Вас и у
Someone, и остальных участников, надо успевать хоть немного учить и всех их))). Должен же быть какой-то баланс.
Вы же, Altenter, пока демонстрируете форуму свою невысокую грамотность в сочетании с высокими претензиями. И если, перефразируя Льва Толстого, рассуждающий о математике человек есть дробь, где его компетентность в числителе, а претензии в знаменателе, то...
Люди всегда недооценивали ноль. Это просто устоявшийся стереотип, сохранившийся в обществе как атавизм)))
-- 29.10.2025, 16:33 --
В отличие от других гипотез, истинность которых также может оказаться неодказуемой, мы видим,
что по крайней мере, ложность опровергается одним контрпримером, например та же, гипотеза Гольдбаха.
А вот с фактом, конечное или бесконечное количество простых-чисел близнецов, совсем по-другому.
Тут что истинность, что ложность, или доказывается аналитически, или не доказывается никогда,
если оно недоказуемо, то никто, даже высшая цивилизация в будущем, за миллиарды лет,
никогда об этом не узнает :)
Недоказуемость существует в рамках представлений. В рамках других представлений ее может и не быть. Поэтому не стоит делать поспешных выводов.