Не уверен, что понимаю сам - в чём претензия к ученику, и какой именно связи он не понимает?
Собственно, ученик знает, что это уравнение надо разделить на

, но не понимает, что это
может привести к потере решений, и требуется как-то этого избежать.
Я бы ответил, что не теряем т.к. решений при
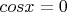
нету. Ну, по мне это должно быть "и так понятно"
За "и так понятно" могут снизить оценку, требуется обоснование.
но формально можно обосновать основным тригонометрическим тождеством. Например:
$sinx=cosx \Leftrightarrow
\begin{cases}
sinx=cosx,}\\
sin^2x+cos^2x=1.}\\
\end{cases}$
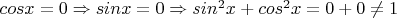
, что противоречит заданной системе.
Ученик как-то так должен был ответить?
Плохое обоснование.
Обосновать можно, например, так.
Проверим, возможны ли решения с

. В этом случае из уравнения

следует, что и

, но тогда
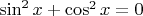
, а это противоречит основному тригонометрическому тождеству. Поэтому все корни заданного уравнения удовлетворяют условию

.
Разумеется, существуют другие способы обоснования и другие способы решения, при которых не нужно делить на выражение, которое может обращаться в

.
Кстати, если бы оказалось, что есть корни, для которых

, то мы могли бы найти эти корни, например, из системы
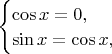
а потом написать "теперь предположим, что

" и спокойно разделить на

, потому что корни с

мы уже нашли.
P.S. Тригонометрические (и не только тригонометрические) функции кодируются с символом "\": \cos x и \lg x дают

и

.