По паттернам без проверяемых мест нашлась и valids=18:
2343924436484807588567979293592713599593860049: 48, 24, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 96, 48, 12, valids=18Одна из наименьших.
-- 18.10.2025, 10:23 --EUgeneUSГенератор паттернов работу закончил, выдал чуть меньше мега текста, наилучшие по Вашим критериям паттерны (показываю по одному с наименьшими коэффициентами при простых):
Код:
0-3-15-3(8), 9шт: v=[ 19, 68, 117, 2, 5, 96, 7, 242, 3, 20, 1, 18, 1, 392, 75, 338, 1, 12, 3179, 3610, 63]
1-1-16-3(8), 138шт: v=[ 5, 68, 63, 2, 1, 480, 13, 242, 3, 28, 5, 18, 1, 8, 1083, 50, 49, 12, 3179, 338, 45]
2-0-15-4(8), 147шт: v=[ 153, 722, 539, 12, 5, 338, 3, 32, 1, 630, 1, 4, 3, 242, 25, 24, 7, 578, 117, 20, 19]
3-0-15-3(8), 4шт: v=[ 14440, 153, 338, 7, 12, 5, 242, 3, 32, 1, 630, 1, 4, 3, 2, 325, 24, 539, 578, 171, 20]
4-0-12-5(8), 44шт: v=[ 14440, 153, 286, 7, 12, 25, 2, 3, 32, 1, 630, 1, 4, 363, 2, 845, 24, 49, 578, 171, 20]
5-0-8-8(8): 99шт: v=[ 504, 1805, 442, 363, 4, 1, 30, 49, 32, 9, 2, 25, 12, 1, 154, 507, 40, 1, 18, 289, 76]
На допустимые остатки не проверял, возможно понадобится замена
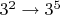
.
Проверил, нужно для всех.

Проверил все 4шт 3-0-15-3(8), да, беда.