Пентадекатлон мечты

[Yadryara]

Yadryara в сообщении #1706095 писал(а):

будет совершенно легальный паттерн? Тогда нет проблем.

Не, ну не так просто оказалось переделать. Но получилось, теперь работает и у меня, и у Демиса.

Посмотрю ещё какие бывают паттерны. А то работы не хватает. Всего 4-5 потоков работают. Чисто интуитивно, выше 1e50 пока не хочется лезть.

[EUgeneUS]

Dmitriy40 в сообщении #1706129 писал(а):

Только поиск такого паттерна будет супермедленным - нет быстрых isprime, придётся сразу запускать медленные factor. Но как концептуальная возможность ...

Если будет хуже (по оценки времени; оценки докуда считать и количество итераций - будет лучше), чем с тремя простыми, то нужно рассматривать с 1 и 2 простыми, сейчас оптимум простых от 0 до 3; 4-ре простых, как понимаю, считаем хуже (по времени), чем три простых.

Можно и четыре простых рассмотреть, если будет паттерн, где количество pqr будет больше 12.

-- 16.10.2025, 19:26 --

Huz в сообщении #1706116 писал(а):

I'm not sure exactly what you need for your Excel file, but if you send me an email with the definition I suspect I can easily provide it as a CSV file. (Keeping up with the forum via translation is hard work.)

Thanks for the offer!
Maybe I'll write later. Or patterns can be generated by Dmitry on his side

[Dmitriy40]

EUgeneUS в сообщении #1706054 писал(а):

1. А существуют ли паттерны типов "4-0-13-4 (9)" и "5-0-13-3 (9)"?

Про эти пока не знаю, зато вот что генератор выдал паттерны 5-0-6-10(9) и 5-0-6-10(8) и 5-0-5-11(8). А ведь у последних двух lcm будет в 59^2=3481 раз меньше, 8.5e39 вместо 3e43, т.е. они более выгодные выходит.

[vicvolf]

EUgeneUS в сообщении #1706064 писал(а):

vicvolf в сообщении #1706060 писал(а):

Для паттерна D(36,15) вероятность того, что случайное $n \leq x$ удовлетворяет паттерну, равна:
$\boxed{P_{\text{pat}}(x) = \frac{\mathfrak{S}(H)}{1{,}307{,}674{,}368{,}000} \cdot \frac{1}{42{,}074{,}422{,}790{,}400 \cdot (\log x)^{15}}}$
где:
- $\mathfrak{S}(H)$ — сингулярный ряд для множества $H$ из 15 сдвигов
- $\log x$ — натуральный логарифм

Тут грубое приближение. В числителе должен быть множитель, зависящий от $\ln (\ln x)$.

Мне кажется, что мы говорим о разном. Не могли бы Вы сформулировать задачу?

[EUgeneUS]

Dmitriy40 в сообщении #1706141 писал(а):

. А ведь у последних двух lcm будет в 59^2=3481 раз меньше, 8.5e39 вместо 3e43, т.е. они более выгодные выходит.

В любом случае нужно собрать статистику и обсчитать один из них, где количество pqr больше.

В первом приближении, по сравнению с 3 простыми:
количество проверок вырастет примерно (несколько меньше) в 25 раз. (Насколько меньше считать надо)
Число, до которого считаем уменьшится примерно в 3481/25 раз, может даже сильнее.

[Yadryara]

Погодите. А точно ничего не путаете? VAL говорил, что меньше 3-х одиночных простых не бывает. Правда, это вроде про D(48,20), а не про D(48,21).

А сейчас промолчал почему-то...

[EUgeneUS]

vicvolf в сообщении #1706142 писал(а):

Мне кажется, что мы говорим о разном

Скорее всего.

vicvolf в сообщении #1706142 писал(а):

Не могли бы Вы сформулировать задачу?

В этой теме обсуждается поиск цепочек последовательных натуральных чисел с одинаковым количеством делителей.

Задача: мы начали искать какую-то такую цепочку, например $D(48, 21)$ - 21 последовательное натуральное число с 48 делителями у каждого.
Вопрос задачи: мы эту цепочку найдем когда? Через месяц или когда звезды потухнут, а черные дыры испарятся?

-- 16.10.2025, 20:37 --

Yadryara в сообщении #1706150 писал(а):

VAL говорил, что меньше 3-х одиночных простых не бывает. Правда, это вроде про D(48,20), а не про D(48,21).

Вот и я откуда-то помню, что меньше трех не бывает....
При увеличение длины минимальное количество простых не может уменьшитлся.

[VAL]

DemISdx в сообщении #1706122 писал(а):

VAL в сообщении #1706058 писал(а):

Кстати, подоспели еще два числа. Для YAFU совсем пустяковые.
Тем более, что если одно разложится как надо, другое можно не трогать (они для одного и того же $k$)
[..]

Готово:
[..]

Отлично!
$M(660) \ge 8$

(Начало цепочки)

n = 178353037164443191420993084423873132384211615394283272657775750588426762431323280921857168222051415675679949991958570238361110179915095057809659628212890621
n + 4 = 5^10 × 29^4 × 59^2 × 18048219939232848996982799577847 × 411007811788710203897049716383490275573432121068325927350694005386181570469828213280067494044813333738314087 
n + 7 = 2^2 × 19^10 × 37^4 × 567603168432476980091953008703632841603775561512865720516291 × 6836483990413877127279034790983327369712289266086653351276391266794364495107

Помнил, что $k=660$ упорно не поддавалось мне 3 года назад.
Но когда заглянул в давние проги, понял, что я почему-то зациклился на поиске цепочек через 8 isprime
Переделал на 4 isprime и все легко нашлось.

[Dmitriy40]

EUgeneUS в сообщении #1706147 писал(а):

Dmitriy40 в сообщении #1706141 писал(а):

. А ведь у последних двух lcm будет в 59^2=3481 раз меньше, 8.5e39 вместо 3e43, т.е. они более выгодные выходит.

В любом случае нужно собрать статистику и обсчитать один из них, где количество pqr больше.

Максимальное значение pqr пока такое: 5+0+8+8(8). Таких паттернов найдено уже 38шт, работа не закончилась. Первый найденный:
v=[ 4, 37791, 2, 25, 24, 1, 98, 363, 20, 1, 18, 1, 32, 105, 338, 1, 12, 1, 31790, 9, 20216];
Чтобы из него получить допустимый по модулю 3 надо правую 9 превратить в 243.

-- 16.10.2025, 22:25 --

EUgeneUS в сообщении #1706152 писал(а):

Вот и я откуда-то помню, что меньше трех не бывает....

Возможно не бывает без вот таких фокусов с $3^5$ ...

-- 16.10.2025, 23:16 --

Поиском по одному паттерну с тремя простыми нашлась одна valids=18 и три valids=17 (ну и 16 несколько):

(Оффтоп)

16948256634087746076068267461645252005741587516704870546: 48, 48, 48, 48, 48, 48, 48, 12, 96, 48, 48, 48, 48, 48, 48, 48, 48,192, 48, 48, 48, valids=18
16644786016901643993575650440389543320200234448955724946: 24, 48, 24, 24, 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 48, 48, 48, 48, 48, 48, 48, valids=17
20925630527640079044678256122035683041455354403224364946: 48, 48, 24, 96, 48, 48, 48, 48, 48, 48,192, 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, valids=17
21641763311941630849890325221249445044529822944029624146: 48, 48, 48, 24, 96, 48, 48, 48, 24, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 96, 48, valids=17

[EUgeneUS]

Dmitriy40 в сообщении #1706155 писал(а):

v=[ 4, 37791, 2, 25, 24, 1, 98, 363, 20, 1, 18, 1, 32, 105, 338, 1, 12, 1, 31790, 9, 20216];
Чтобы из него получить допустимый по модулю 3 надо правую 9 превратить в 243.

Запустил расчет статистики по паттерну

v=[ 4, 37791, 1058, 25, 20184, 961, 98, 363, 20, 1369, 18, 1681, 32, 194145, 338, 2209, 12, 2809, 31790, 243, 20216];\\ 5+0+8+8(8)
nd=48;\\Количество делителей
pr2=primes([5,53]);\\Эти квадраты размещены
ip=20;\\Перебирать будем по месту +20

Прогнозирует 13-14 часов, вместо 20-21 часа для 9 необязательных простых в квадрате.
Это эффект от улучшения скорости факторизации на менее размерных числах.
Считается тут:

i1=round(1e7); i2=i1+round(1e5);\\Интервал счёта, справа не включая

В боевом расчете числа будут более размерными. Так что этот эффект может нивелироваться.

[Yadryara]

VAL в сообщении #1704105 писал(а):

EUgeneUS в сообщении #1704102 писал(а):

полусотня VS треть миллиона (и только на перестановках минимальных необязательных простых)

Ну извините, миллиона логических ядер на моих 4-х компах не нашлось

Ну так и необязательно огромное количество логических ядер, ведь был придуман способ как обсчитывать тысячи паттернов в одном потоке.

Давайте, кстати, взглянем на обновлённую таблицу лучших приближений к D(48,21):

Start                                                     Location              Valids
17668887847524548413038893976018715843277693308027547     11111111111111111111      20  VAL
26775093546337571754412744723988589091340703171346        1111111 1111111111 11     19  An
85214054718602387929373909199904790013177732572016804946  1111111 1111111111 11     19  VAL
51684540038790306040313810619606026245800104809434        11 111111 1111111 111     18  An
72909466110460584674297272553362643585315288960146        1111111 1111 11 11111     18  An
82702393061651749407237510142718298553252873153434        1 11 11111111 1111111     18  An
154631495973083613535277148109710834053326309716946       111  11111111111111 1     18  An
585605360962144936768057576267008749038198122219346       1111111 111 1111111 1     18  An
606402818949710702556903161178143151197645296548946       11111 1 1111111111 11     18  An
628680904801738074581702744562430440461822260856146       11111 111111111 111 1     18  An
7463656036994854901626760003614676193212978675835346      111111111  1111 11111     18  An
16948256634087746076068267461645252005741587516704870546  1111111  11111111 111     18  Dm
29825395661688231658603848650736899419196053570174356946  111111111111111 11  1     18  VAL
90715763859608616730714175556209422588238079327693680146  1111111111111111 1  1     18  VAL

Видите большущую разницу в величине чисел? Так вот, маленькие числа найдены именно этим многопаттерным способом.

[vicvolf]

VAL в сообщении #1706081 писал(а):

vicvolf в сообщении #1706074 писал(а):

Мне не удалось найти интернет-источники, которые подтверждают это конкретное обозначение или упомянутую вами статью Дюнша и Эгглтона 1989 года.

ссылка

Спасибо! Ознакомился со статьей. Интересно, но там нет вывода асимтотик количества цепочек и вероятности, поэтому пришлось сделать.

Оценка вероятности существования цепочек чисел с одинаковым числом делителей

Постановка задачи
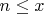
Рассмотрим задачу о нахождении цепочек последовательных натуральных чисел, имеющих одинаковое фиксированное количество делителей. Формально: для заданных натуральных чисел $ k $ и $ m $ мы хотим оценить вероятность того, что для случайного $ n \leq x $ выполняется:
$d(n) = d(n+1) = \cdots = d(n+m-1) = k$
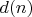
где $ d(n) $ — число положительных делителей $ n $.

Вывод формул:
1. Асимптотика для одного числа
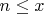
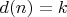
Известный результат в аналитической теории чисел утверждает, что для фиксированного $ k $ количество чисел $ n \leq x $ с $ d(n) = k $ имеет асимптотику:
$N_k(x) \sim C_k \cdot x \cdot \frac{(\log\log x)^{a(k)}}{\log x}$
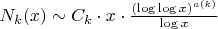
где:
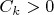
- $ C_k > 0 $ — постоянная, зависящая от мультипликативной структуры $ k $
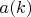
- $ a(k) $ — неотрицательное целое число, определяемое разложением $ k $ на простые множители
Вероятность для одного числа:
$P_1(k) = \frac{N_k(x)}{x} \sim C_k \cdot \frac{(\log\log x)^{a(k)}}{\log x}$

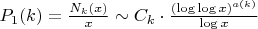
2. Наивная оценка (предположение о независимости)
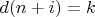
Если бы события $ d(n+i) = k $ были независимы для разных $ i $, то вероятность цепочки длины $ m $ оценивалась бы как:
$P_{\text{naive}}(m,k) \sim \left[C_k \cdot \frac{(\log\log x)^{a(k)}}{\log x}\right]^m$

3. Учёт локальных зависимостей
На самом деле, числа в цепочке тесно связаны арифметическими зависимостями, которые влияют на вероятность. Основные источники зависимостей:
Структурные ограничения на показатели степеней
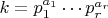
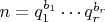
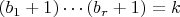
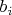
Число с фиксированным $ k $ делителями имеет жёсткую структуру. Если $k = p_1^{a_1} \cdots p_r^{a_r}$, то $n = q_1^{b_1} \cdots q_r^{b_r}$, где $ (b_1+1)\cdots(b_r+1) = k $. Показатели $ b_i $ жёстко зафиксированы.

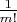
Появляется комбинаторный множитель $ \frac{1}{m!} $- учёт неразличимости структур при распределении простых чисел по позициям в цепочке.

Локальные корреляции от малых простых
Малые простые создают сильные корреляции между соседними числами:
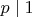
- Запрет одинаковых простых делителей: Если $ n $ и $ n+1 $ оба делятся на простое $ p $, то $ p \mid 1 $ — невозможно
-Структурные условия делимости: Для данного $ k $ возможны только определённые комбинации показателей
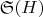
Появляется сингулярный ряд $ \mathfrak{S}(H) $, учитывающий корреляции между разными позициями:
$\mathfrak{S}(H) = \prod_p \frac{\gamma_p(H)}{(1 - 1/p)^m}$
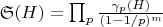
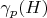
где $ \gamma_p(H) $ — вероятность, что все числа в цепочке "проходят" локальные условия по модулю $ p $.

Арифметические прогрессии с запретами
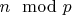
Для каждого малого простого $ p $ некоторые остатки $ n \mod p $ запрещены.

Вычисления:
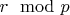
1. Для фиксированного $ k $ определяем, какие остатки $ r \mod p $ возможны для чисел с $ d(n) = k $
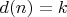
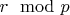
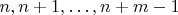
2. Находим остатки $ r \mod p $, для которых ВСЕ числа $ n, n+1, \ldots, n+m-1 $ удовлетворяют индивидуальным условиям
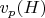
3. $ v_p(H) $ = количество запрещённых остатков $ r \mod p $

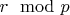
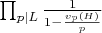
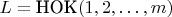
Получаем поправочный множитель $ \prod_{p \mid L} \frac{1}{1 - \frac{v_p(H)}{p}} $, где $ L = \text{НОК}(1, 2, \ldots, m) $ — параметр, определяющий множество малых простых, по которым учитываются локальные зависимости.

Объединяя все поправки, получаем эвристическую формулу:
$\boxed{P(m,k) \sim \frac{\mathfrak{S}(H)}{m!} \cdot \left[C_k \cdot \frac{(\log\log x)^{a(k)}}{\log x}\right]^m \cdot \prod_{p \mid L} \frac{1}{1 - \frac{\nu_p(H)}{p}}}$

Пример: D(48,21)
Исходные данные:
- $ k = 48 $, $ m = 21 $, $ x = 10^{50} $
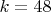
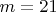
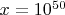
- Для $ k = 48 $: $ a(48) = 4 $, $ C_{48} \approx 0.1 $
- $ L = \text{НОК}(1,2,\ldots,21) = 232{,}792{,}560 $

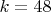
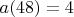
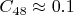
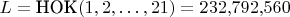
Вычисление параметров:
- $ \log x = \log(10^{50}) = 50 \cdot \log 10 \approx 115.13 $
- $ \log\log x = \log(115.13) \approx 4.746 $
- $ 21! \approx 5.1 \times 10^{19} $

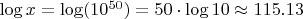
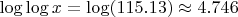
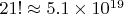
1. Вероятность одного числа
$P_1(48) \sim 0.1 \cdot \frac{(4.746)^4}{115.13}$
$4.746^2 \approx 22.52,\quad 4.746^4 \approx 507.0$
$P_1(48) \approx 0.1 \cdot \frac{507.0}{115.13} \approx 0.1 \cdot 4.404 \approx 0.4404$

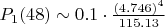
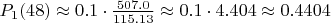
2. Наивная оценка цепочки
$P_{\text{naive}} \sim (0.4404)^{21}$
$\log_{10}(P_{\text{naive}}) = 21 \cdot \log_{10}(0.4404) = 21 \cdot (-0.3562) \approx -7.48$
$P_{\text{naive}} \approx 10^{-7.48} \approx 3.31 \times 10^{-8}$

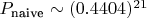
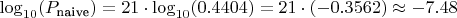
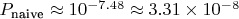
3. Учёт зависимостей
Оценим поправочные множители:
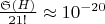
- $ \frac{\mathfrak{S}(H)}{21!} \approx 10^{-20} $ (сильные структурные ограничения для m=21)
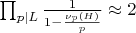
- $ \prod_{p \mid L} \frac{1}{1 - \frac{\nu_p(H)}{p}} \approx 2 $ (учёт влияния малых простых)

Итоговая вероятность:
$P(48,21) \sim 10^{-20} \cdot 3.31 \times 10^{-8} \cdot 2 \approx 6.62 \times 10^{-28}$

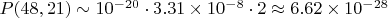
4. Ожидаемое количество цепочек
$N_{\text{expected}} \sim x \cdot P(48,21) = 10^{50} \cdot 6.62 \times 10^{-28} \approx 6.62 \times 10^{22}$

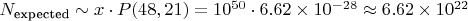
Выводы:
Для D(48,21) в диапазоне до $ 10^{50} $:
$P(48,21) \sim 6.6 \times 10^{-28}$
$N_{\text{expected}} \sim 6.6 \times 10^{22} \text{ цепочек}$
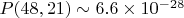
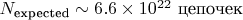
- Цепочка D(48,21) почти наверняка существует в этом диапазоне
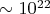
- Ожидается огромное количество экземпляров ($ \sim 10^{22} $).

[Yadryara]

Хорошие новости надо сообщать сразу, чего же тянуть кота за резину.

Yadryara в сообщении #1706051 писал(а):

Моё время счёта — 38 часов.

Я думал. что у Демиса займёт 25-30 часов. Ан нет — уложился в 10 часов в один поток!!

Вот такая штука практика.

Так что очередь за компом VALа. Не о 32-х потоках речь идёт, а об одном, для теста. 7-й или 8-й зеркальный комплект на выбор. Программа уже готова, её только запустить на PARI.

И кстати, VAL, вопрос Дмитрия тоже не заметили?

[Dmitriy40]

EUgeneUS в сообщении #1706128 писал(а):

Dmitriy40 в сообщении #1706117 писал(а):

v=[ 9, 50, 49, 12, 289, 338, 1815, 2888, 1, 126, 1, 20, 3, 2, 1, 96, 35, 22, 117, 4, 1]

чудо какое
Надо статистику на него напустить. А как, если там нет простых?

И однако в этом чуде 0-6-7-8(8) тоже находятся цепочки! Запускал на ночь, чистый PARI, медленно, но нашлись 8 цепочек, из которых одна даже valids=17:
96100031146543695632608418489278806868523936309649: 28, 48, 48, 48, 48, 48, 48, 48, 48, 48, 24, 48, 24, 48, 48, 48, 48, 48, 48, 24, 48, valids=17
Остальные vailds=10-14.
Скорость перебора 60с на 1e6 значений i, при m=lcm(v)=2.294e41, т.е. 3.8e45/с.

С паттерном 5-0-8-8(8) тоже нашлись две длинные цепочки:
839959258412050706582280265714599432746929162531861405650: 48, 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 24, 48, 24, 48, 48, 48, 24, 48, 48, 48, valids=17
1011988149789983961687458524958725118967506966040950548050: 48, 48, 96, 48, 48, 96, 48, 48, 48, 24, 48, 24, 96, 48, 48, 48, 48, 48, 48, 48, 48, valids=16
Остальные 10шт valids=8-14.

Ну и в 3-0-13-5(9) нашлась 4-я valids=17:
39256746417897062753293437800667770183999173850948787346: 48, 48,192, 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 12, 48, 48, 48, 48, 48, 24, 48, valids=17

[EUgeneUS]

Dmitriy40 в сообщении #1706177 писал(а):

И однако в этом чуде 0-6-7-8(8) тоже находятся цепочки! Запускал на ночь, чистый PARI, медленно, но нашлись 8 цепочек, из которых одна даже valids=17:
96100031146543695632608418489278806868523936309649: 28, 48, 48, 48, 48, 48, 48, 48, 48, 48, 24, 48, 24, 48, 48, 48, 48, 48, 48, 24, 48, valids=17
Остальные vailds=10-14.
Скорость перебора 60с на 1e6 значений i, при m=lcm(v)=2.294e41, т.е. 3.8e45/с.

А куда бы они делись?
В этом паттерне цепочек будет раз в $5^3=125$ больше, чем в паттерне с 3 простыми. В расчете на тот же диапазон $i$.
Оценка наивная, завышенная, но думаю раз в 100 будет.
Можете скинуть готовый такой паттерн (с расставленными квадратами простых, и правильной степенью тройки)?
А я вечером поставлю сбор статистики и на выходных посчитаю его.

-- 17.10.2025, 12:49 --

а с 1 и 2 простыми что-то интересное из паттернов не нашлось?

-- 17.10.2025, 13:04 --

vicvolf в сообщении #1706167 писал(а):

Постановка задачи
Рассмотрим задачу о нахождении цепочек последовательных натуральных чисел, имеющих одинаковое фиксированное количество делителей. Формально: для заданных натуральных чисел $ k $ и $ m $ мы хотим оценить вероятность того, что для случайного $ n \leq x $ выполняется:
$d(n) = d(n+1) = \cdots = d(n+m-1) = k$
где $ d(n) $ — число положительных делителей $ n $.

Теперь мы говорим о близком, но всё равно о разном.
Следующий шаг: цепочки ищутся не просто так, а заведомо неподходящие откидываются с помощью расстановок обязательных простых и применения китайской теоремы об остатках. Для дальнейшего чтения:

A119479, A292580 и статьи разделе LINKS к этим последовательностям.