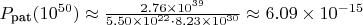Пентадекатлон мечты

[EUgeneUS]

Dmitriy40
Про хорошие паттерны и тренды на рынке цепочек (chain market ).

Удобное обозначение типа паттерна: "3-0-13-5 (9)" - 3 простых, 0 pq, 13 prq, 5 pqrs, 9 (необязательных) простых в квадратах.
Далее буду его использовать.
1. В первом приближении:
Для $D(48,21)$ типовые вероятности для одного места при некоторых больших $N$:

P(p)     0.066167291
P(pq)   0.206491885
P(pqr)   0.314107366
P(pqrs)   0.22247191

2. Переход от паттерна "3-0-13-5 (9)" к "4-0-12-5 (9)" означает, что в какой-то позиции вместо $0.314$ будет $0.066$, что в $4.76$ раза меньше.
То есть цепочки будут находиться в $4.76$ раза реже, а считать нужно будет в $4.76$ дальше.
Во втором приближении работает падение вероятности с ростом $N$, и оказывается, что считать надо примерно в $5.4$ раза дальше.

3. Теперь предположим, что существует паттерн типа "4-0-13-4 (9)", это будет означать, что в какой-то позиции вместо $0.222$ будет $0.066$, что уже в $3.63$ раза меньше. Со всеми предлагающимися "плюшками".

4. И аналогично для паттернов с пять простыми.
Предлагаемый паттерн на пять простых имеет тип $5-1-8-7 (9)$. То есть не только одно хорошее pqr на p заменилось, но и куча хороших pqr заменились на нехорошие pq и pqrs.
С пятью простыми хорошим будет паттерн типа "5-0-13-3 (9)"

Остаются открытыми вопросы:
1. А существуют ли паттерны типов "4-0-13-4 (9)" и "5-0-13-3 (9)"?
2. А может быть, для четырех и пяти простых существуют ещё лучшие паттерны, с ещё большим количеством $pqr$?

По-хорошему, надо бы:
1. Построить pcoul'ом полную систему паттернов.
2. Выкинуть из них паттерны "с неизвестными квадратами" (они кстати, метятся в выводе pcoul'а).
3. Оставшиеся загнать в какой-нибудь скрипт, который посчитает для паттернов lcm и тип в нотации "5-0-13-3 (9)".

Такое делал три года назад для $D(15,36)$ и $D(15,12)$. Сейчас для $D(48,21)$ останавливает следующее:
1. Паттернов, предполагаю, будут какие-то невообразимые сотни миллионов. И вывод pcoul'а сожрет все место на "счетах" (там несколько сотен Мб осталось сейчас )
2. Не нашел в архивах (после чисток ) виндовую версию pcoul.
3. Для $D(15,36)$ и $D(15,12)$ типизировал паттерны в полуручном режиме в Экселе, и, насколько помню, подз... подустал это делать.

[Yadryara]

VAL
Ну я понял, у Вас был трудный выбор. Выделить один поток вроде мало. А два — уже не хочется.

Так что да, теперь уже выбирайте между 2-мя и 3-мя. Между двумями и тремями

А пока думаете, у меня один поток освободился и я 8-й комплект запустил считаться. 9-й пока вакантен.

[EUgeneUS]

Для примера:

1. Кусок вывода pcoul для $D(15,36)$

001 pcoul(36 15) -f13 -x1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 *RT*
203 b0: 2^8.3 5 2.11^8 3.13^8 2^2.7 . 2.3^2.5^2 . 2^3 3 2 5.7^8 2^2.3 11 2 [sq=1]
203 b1: 2^8.3 5 2.11^8 3.13^2 2^2.7 . 2.3^2.5^2 . 2^3 3 2 5.7^8 2^2.3 11 2 [sq=1]

Сырой результат работы pcoul для $D(15,36)$ - 25 Мб.

2. Кусок уже "типизированных" паттернов:

=;ID;1;2;3;4;5;6;7;8;9;10;11;12;13;14;15;2;3;5;7;11;13;LCM;1;2;3;4;5;6;7;8;9;10;11;12;13;14;15;pq
203;b18825:;3^8;2.7^2;11.13^2;2^2.3;5;2;3;2^8;7;2.3^2.5^2;.;2^2;3;2.11^2;5;8;8;2;2;2;2;42074422790400;pq;p;p;p;p;p;p;pq;p;p;pq;pq;p;p;p;4
203;b18826:;3^8;2.7^2;11;2^2.3.13^2;5;2;3;2^8;7;2.3^2.5^2;.;2^2;3;2.11^2;5;8;8;2;2;2;2;42074422790400;pq;p;p;p;p;p;p;pq;p;p;pq;pq;p;p;p;4

Только тогда не считал напрямую количество необязательных простых в квадрате.

-- 16.10.2025, 09:35 --

Yadryara в сообщении #1706055 писал(а):

у меня один поток освободился и я 8-й комплект запустил считаться. 9-й пока вакантен.

Сообщите товарищам - а сколько вообще будет "комплектов"

[VAL]

DemISdx
Как там дела с

(2 prime factors wanted)

1333401164884342191362652252579505933409163456046203884330678826542919483592953731718836518733790256578836971646812287941080692080294389337741328644132777 (154 digits) = pq?

?
Кстати, подоспели еще два числа. Для YAFU совсем пустяковые.
Тем более, что если одно разложится как надо, другое можно не трогать (они для одного и того же $k$)

(2 prime factors wanted)

3880409973896820239227497169313840857498544480513383386846750680906144024741982113907070533030961378371860775088753842277017271583288137 (136 digits) = pq?

(2 prime factors wanted)

1911445084584925875980446689735740735252481458318729578236426900705904873937145996083151352755502688937090727859165606402025838498148927  (136 digits) = pq?

-- 16 окт 2025, 09:40 --

Yadryara в сообщении #1706055 писал(а):

VAL
Ну я понял, у Вас был трудный выбор. Выделить один поток вроде мало. А два — уже не хочется.

Ошибаетесь.
Выбор был между 20-ю, 32-я и 40-а.
Но позже.

-- 16 окт 2025, 09:41 --

EUgeneUS в сообщении #1706054 писал(а):

1. А существуют ли паттерны типов "4-0-13-4 (9)" и "5-0-13-3 (9)"?
2. А может быть, для четырех и пяти простых существуют ещё лучшие паттерны, с ещё большим количеством $pqr$?

Поищу.

[Yadryara]

EUgeneUS в сообщении #1706056 писал(а):

Сообщите товарищам - а сколько вообще будет "комплектов"

Сообщите когда перестанете злобные смайлики ставить.

Комплектов у меня больше нет. Надо обязательную программу перестраивать, или хотя бы отзеркалить имеющийся паттерн. Тогда появятся ещё 9 комплектов по 40320 паттернов.

[vicvolf]

Эвристический вывод асимптотики вероятности для смешанных кортежей

Постановка задачи и обозначения
Рассматривается смешанный кортеж длины $k$, где:
- $I$ — множество индексов простых элементов, $|I| = m$
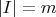
- $J$ — множество индексов составных элементов, $|J| = k-m$
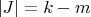
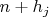
- Для каждого $j \in J$: число $n + h_j$ должно делиться на фиксированное число $d_j > 1$
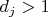
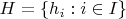
- $H = \{h_i : i \in I\}$ — множество сдвигов для простых позиций
- $L = \mathrm{lcm}\{d_j : j \in J\}$
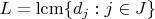
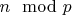
- Паттерн считается допустимым, если для каждого простого $p$ существует решение $n \mod p$, удовлетворяющее всем условиям

Основа: классическая гипотеза Харди-Литлвуда
Для кортежа из $m$ простых чисел Харди и Литтлвуд предложили асимптотику:
$N_{\text{HL}}(x) \sim \frac{\mathfrak{S}(H)}{m!} \cdot \frac{x}{(\log x)^m}$
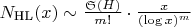
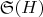
где сингулярный ряд $\mathfrak{S}(H)$ учитывает локальные зависимости:
$\mathfrak{S}(H) = \prod_p \left(1 - \frac{\nu_p(H)}{p}\right) \left(1 - \frac{1}{p}\right)^{-m}$
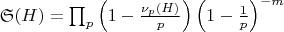
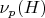
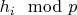
и $\nu_p(H)$ — количество различных вычетов $h_i \mod p$ для $i \in I$.

Модификация для смешанных кортежей
1. Учёт условий на составные позиции
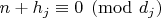
Условия $n + h_j \equiv 0 \pmod{d_j}$ для $j \in J$ эквивалентны системе сравнений:
$n \equiv a \pmod{L}, \quad L = \mathrm{lcm}\{d_j\}$
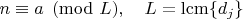
Для случайного $n$ вероятность выполнения этих условий:
$\mathbb{P}(\text{условия на } J) = \frac{1}{L}$

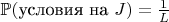
2. Условная вероятность простоты
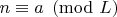
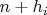
При условии $n \equiv a \pmod{L}$, мы хотим, чтобы числа $n + h_i$ для $i \in I$ были простыми.
Наивная эвристика: если бы события были независимы, вероятность была бы:
$\mathbb{P}_{\text{naive}} = \frac{1}{(\log x)^m}$

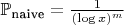
3. Поправка на локальные зависимости
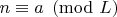
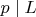
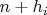
Условие $n \equiv a \pmod{L}$ уже гарантирует, что для простых $p \mid L$ ни одно $n + h_i$ не делится на $p$ (по построению допустимого паттерна).
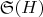
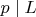
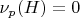
В сингулярном ряде $\mathfrak{S}(H)$ для $p \mid L$ имеем $\nu_p(H) = 0$, поэтому:
$\text{Множитель для } p \mid L = \frac{1}{\left(1 - \frac{1}{p}\right)^m}$
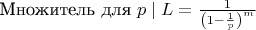
Это та поправка, которая нужна для перехода от безусловной вероятности к условной.

4. Нормировочный множитель $1/m!$
Множитель $1/m!$ возникает из-за упорядочивания:
- Мы считаем вероятности для конкретного набора $h_1, \dots, h_m$
- В комбинаторных выкладках это естественная нормировка

Итоговая формула
Собирая все множители:
1. Вероятность условий на составные позиции: $\frac{1}{L}$
2. Наивная вероятность простоты $m$ чисел: $\frac{1}{(\log x)^m}$
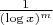
3. Поправка на локальные зависимости: $\mathfrak{S}(H)$
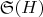
4. Нормировочный множитель: $\frac{1}{m!}$
Получаем:
$P_{\text{pat}}(x) \sim \frac{\mathfrak{S}(H)}{m!} \cdot \frac{1}{L (\log x)^m}$

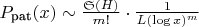
Предложенная асимптотика является естественным обобщением гипотезы Харди-Литлвуда на смешанные кортежи и основана на:
1. Вероятностной интерпретации простых чисел
2. Учёте локальных условий через китайскую теорему об остатках
3. Поправке на зависимости через сингулярный ряд
4. Нормировке на симметрию кортежа

В качестве примера рассмотрим расчет вероятности для паттерна D(36,15)
Исходные данные
- Паттерн: D(36,15) — 36 элементов, из которых 15 простых, 21 составной
- Обязательные делители: $2^8, 3^8, 5^2, 7^2, 11^2, 13^2$
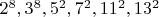
- Количество простых элементов: $m = 15$

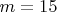
Вычисление параметра $L$
- $256 \cdot 6561 = 1{,}679{,}616$
- $1{,}679{,}616 \cdot 25 = 41{,}990{,}400$
- $41{,}990{,}400 \cdot 49 = 2{,}057{,}529{,}600$
- $2{,}057{,}529{,}600 \cdot 121 = 248{,}961{,}081{,}600$
- $248{,}961{,}081{,}600 \cdot 169 = 42{,}074{,}422{,}790{,}400$
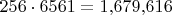
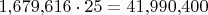
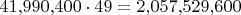
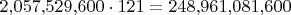
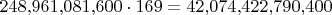
Итог:
$L = 42{,}074{,}422{,}790{,}400$

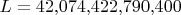
Вычисление факториала
$15! = 1 \cdot 2 \cdot 3 \cdots 15 = 1{,}307{,}674{,}368{,}000$

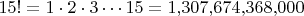
Итоговая формула вероятности
Для паттерна D(36,15) вероятность того, что случайное $n \leq x$ удовлетворяет паттерну, равна:
$\boxed{P_{\text{pat}}(x) = \frac{\mathfrak{S}(H)}{1{,}307{,}674{,}368{,}000} \cdot \frac{1}{42{,}074{,}422{,}790{,}400 \cdot (\log x)^{15}}}$
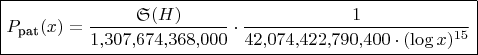
где:
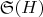
- $\mathfrak{S}(H)$ — сингулярный ряд для множества $H$ из 15 сдвигов
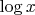
- $\log x$ — натуральный логарифм

Упрощенная форма
$P_{\text{pat}}(x) = \frac{\mathfrak{S}(H)}{5.50 \times 10^{22} \cdot (\log x)^{15}}$

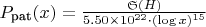
Пример численной оценки
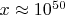
Для $x \approx 10^{50}$ (типичное значение в поисках кортежей):
- $\log x \approx 115.13$
- $(\log x)^{15} \approx 8.23 \times 10^{30}$
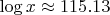
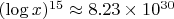
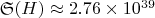
Если $\mathfrak{S}(H) \approx 2.76 \times 10^{39}$ (оценка из экспериментальных данных):
$P_{\text{pat}}(10^{50}) \approx \frac{2.76 \times 10^{39}}{5.50 \times 10^{22} \cdot 8.23 \times 10^{30}} \approx 6.09 \times 10^{-15}$

[Yadryara]

Yadryara в сообщении #1706059 писал(а):

отзеркалить имеющийся паттерн.

Может даже проще будет напрямую спросить у VAL. Вот у меня есть болванка, полученная после обязательной программы по простым 2, 3, ... ,19.

M = [2, 3971,12,49,50, 3 ,104, 1 ,18, 5 ,28, 3 ,242, 1 ,480,289, 2 ,63, 4 ,845,114]

Как получить зеркальную болванку? Напишите, пожалуйста, прямо здесь, Эксель ни к чему.

-- 16.10.2025, 10:27 --

vicvolf в сообщении #1706060 писал(а):

В качестве примера рассмотрим расчет вероятности для паттерна D(36,15)
Исходные данные
- Паттерн: D(36,15) — 36 элементов, из которых 15 простых, 21 составной

Шутить изволите?

Здесь же не кортежная тема. И запись D(36,15) означает цепочку из 15 последовательных натуральных чисел, где каждое число имеет ровно 36 делителей. Это обозначение использовалось ещё в работе Дюнша и Эгглтона (фамилии по памяти) 1989 года.

[EUgeneUS]

vicvolf в сообщении #1706060 писал(а):

Эвристический вывод асимптотики вероятности для смешанных кортежей

Примерно так оно и строилось.

vicvolf в сообщении #1706060 писал(а):

Для паттерна D(36,15) вероятность того, что случайное $n \leq x$ удовлетворяет паттерну, равна:
$\boxed{P_{\text{pat}}(x) = \frac{\mathfrak{S}(H)}{1{,}307{,}674{,}368{,}000} \cdot \frac{1}{42{,}074{,}422{,}790{,}400 \cdot (\log x)^{15}}}$
где:
- $\mathfrak{S}(H)$ — сингулярный ряд для множества $H$ из 15 сдвигов
- $\log x$ — натуральный логарифм

Тут грубое приближение. В числителе должен быть множитель, зависящий от $\ln (\ln x)$.

-- 16.10.2025, 10:38 --

Yadryara в сообщении #1706059 писал(а):

Сообщите когда перестанете злобные смайлики ставить.

Это же веселые смайлики, а не злобные.

Yadryara в сообщении #1706059 писал(а):

Комплектов у меня больше нет.

Вы до каких чисел всё посчитали\посчитаете этими 9-ю комплектами?

Yadryara в сообщении #1706059 писал(а):

Надо обязательную программу перестраивать, или хотя бы отзеркалить имеющийся паттерн.

Увеличение паттернов в два раза:
а) уменьшит число, до которого надо считать примерно в 2 раза.
б) крайне мало отразится на количестве необходимых проверок.
Нету смысла.

Что-то можно получить в виде снижения количество попыток раза в два при увеличении количества паттернов до $30000000 ... 100000000$, то есть на 2-2.5 порядка .

-- 16.10.2025, 10:56 --

vicvolf в сообщении #1706060 писал(а):

$P_{\text{pat}}(10^{50}) \approx \frac{2.76 \times 10^{39}}{5.50 \times 10^{22} \cdot 8.23 \times 10^{30}} \approx 6.09 \times 10^{-15}$

По моим расчетам, для $x=10^{50}$ получается $P= 1.20 \cdot 10^{-14}$.
И не думаю, что ошибсяя на потора порядка (хотя для этого паттерна статистика не собиралась).

[vicvolf]

Yadryara в сообщении #1706063 писал(а):

Здесь же не кортежная тема. И запись D(36,15) означает цепочку из 15 последовательных натуральных чисел, где каждое число имеет ровно 36 делителей. Это обозначение использовалось ещё в работе Дюнша и Эгглтона (фамилии по памяти) 1989 года.

Мне не удалось найти интернет-источники, которые подтверждают это конкретное обозначение или упомянутую вами статью Дюнша и Эгглтона 1989 года.

[VAL]

Yadryara в сообщении #1706063 писал(а):

M = [2, 3971,12,49,50, 3 ,104, 1 ,18, 5 ,28, 3 ,242, 1 ,480,289, 2 ,63, 4 ,845,114]

Как получить зеркальную болванку? Напишите, пожалуйста, прямо здесь, Эксель ни к чему.

Кто-то из нас чего-то недопонимает...
Отзеркаливание в моем понимании это ... отзеркаливание, то есть прочтение справа налево.
Но, судя по Вашему вопросу, Вы вкладываете в это слово какой-то другой смысл.

-- 16 окт 2025, 11:51 --

vicvolf в сообщении #1706074 писал(а):

Мне не удалось найти интернет-источники, которые подтверждают это конкретное обозначение или упомянутую вами статью Дюнша и Эгглтона 1989 года.

ссылка

[DemISdx]

VAL в сообщении #1706058 писал(а):

DemISdx
Как там дела с
(2 prime factors wanted)
Код:

133340...32777 (154 digits) = pq?


?

VAL
Дела с 133340... - отлично:

(Оффтоп)

Дык это https://dxdy.ru/post1705799.html#p1705799
Просто народ очень много сообщений пишет и возможно оное просто мимо глаз проскочило...
Перепроверьте пожалуйста меня.

[VAL]

DemISdx в сообщении #1706087 писал(а):

Дела с 133340... - отлично:
[..]

Действительно проморгал
Спасибо!
Сейчас опишу получившуюся цепочку. Рекордную, не по размеру $k$, а...
В общем, сейчас.

[Yadryara]

EUgeneUS в сообщении #1706064 писал(а):

Вы до каких чисел всё посчитали\посчитаете этими 9-ю комплектами?

Расст.    Посчитано от 0 до   Коментарий

123                    1e52   Завершено  
1                      1e51   Сегодня завершится
2 — 9                  1e50   Послезавтра завершится

[VAL]

$M(552) \ge 8$

(Начало цепочки)

n = 490798861251672257003214051133839421207413525566074423680729685784858902235793481298737052049880445037723178091570414808357594028301046295578252592991472387784585820430974960327148437498
n+2 = 2^2 × 5^22 × 77599361503 × 19640891703820119010317119447713 × 33766349459040185317597539189189330327156765902136373174899545516103598944318183689238288475393574579054984664618139579222096057
n+5 = 11^22 × 29^2 × 5 376599 ×  × 306794534268386049862799051689211478061173594553881696742193193592261 × 4346235072486243605901118255844380291356365323519747900072897927309335973876692599957
n+6 = 2^22 × 37^2 × 24644987 × 18150189571433611363677175774820687 × 191086688760733415656979277051671695770094551965009441695073190686274471683176419988065422651918496225951999223555384717518096873302441

В чем рекорд?

522 кратно 23. Каждое из 8-и чисел цепочки делится на 22-ю степень какого-то простого числа.
Столь больших обязательных степеней для столь длинных цепочек у нас еще не было.

[EUgeneUS]

Yadryara
Вероятность найти цепочку (для текущей схемы расчета), если считать все $9!$ шаблонов:

до $10^{50}$, $P(\text{win}) = 0.00267$
до $10^{51}$, $P(\text{win}) = 0.02054$
до $10^{52}$, $P(\text{win}) = 0.14865$
до $10^{53}$, $P(\text{win}) = 0.71510$
до $10^{54}$, $P(\text{win}) = 0.99994$