За ночь ради интереса перебрал все 9! вариантов до 5e48, заняло 10.5ч.
Самые длинные:
Код:
14-78462 4054427843685007678761054689486739499279168620946 111 1111 1 11111 11 1 16 [2, 9, 5, 8, 7, 1, 6, 4, 3]
49-276358 1609770849692896063285412871371657574193960875346 1 1 11111 1111111 11 16 [7, 8, 6, 5, 9, 4, 2, 3, 1]
10-70334 675316765727137388857296968791369010581278046546 1 11111111 1 11111 15 [2, 7, 9, 6, 1, 5, 3, 8, 4]
22-127083 3426281091350161357284426644686896276386601483346 1 111111111 1 111 1 15 [4, 2, 3, 7, 1, 5, 8, 6, 9]
25-134288 2581791426301369099934560090141163977369909438546 1 11 11 1 111111 11 1 15 [4, 3, 7, 6, 1, 5, 2, 9, 8]
31-177706 1777730187070289597223879408604491923932932819346 1111 111 11 11111 1 15 [5, 4, 2, 8, 9, 3, 6, 7, 1]
34-196681 385236555204379860040700086316757403359126675346 1 1 111 111 11 11111 15 [5, 9, 1, 3, 2, 4, 6, 7, 8]
35-197370 4782169045122473198930066445070685279518093116946 111 1 1111 1111111 15 [5, 9, 2, 1, 7, 6, 8, 4, 3]
42-227385 4888462525191848396632635165082679532714444488146 1111111 1 11 1 11 11 15 [6, 7, 1, 8, 9, 3, 4, 2, 5]
44-239119 1203184497465162855348104603765014756231359420946 1 1 111 11 11 11 1111 15 [6, 9, 4, 1, 7, 3, 2, 5, 8]
51-286154 2105106151650200055785788743993643318789327414546 11 1 11 111 1 11 1111 15 [8, 1, 7, 4, 6, 2, 3, 9, 5]
59-342149 2118533566899845201784331597262560551434157224146 11 11111 11111 1 11 15 [9, 4, 8, 2, 3, 1, 7, 5, 6]
Для больших чисел программа перебирает заметно быстрее, чем для меньших!
А с ускорителями такого не должно быть - здесь "виноваты" ранние isprime, которые для больших чисел отбраковывают кандидатов чаще (невзирая на замедление проверки каждого этими же isprime), ускорители же работают в остатках по модулям, которые не зависят от величины чисел.
-- 15.10.2025, 13:44 --10 минут на проверку 9! паттернов в диапазоне

А для вероятности 0.95 нужно
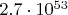
Это 51369 потоко-лет.


Это не слишком корректно, у меня что 1e45, что 1e46, перебираются одинаковое время, 1e47 всего вдвое дольше, и только дальше время растёт линейно - т.е. до 1e48 время тратится не на факторизацию, а до 1e47 и не на проверку паттернов. Потому что поставив next перед foreach(ost,dd, получим время работы внешнего цикла 5 минут для 1e47, а поставив next на две строки ниже перед forstep(i=sta+dd,sto,shag, получим время 13 минут для 1e47, почти как и для проверки 1e45 и 1e46 (т.е. по 1e46 проверка почти бесплатная).
Я же специально сделал Вам вывод ETA чтобы за несколько минут (по первым десяткам размещений, по первым единицам сильно ошибается) оценить общее требуемое время и не ждать часами и сутками для выяснения какая скорость проверки.
У меня до 2.7e48 собирается работать 6ч40м, значит до 2.7e53 надо 666667ч=76г. А оценка за ночь 10.5ч на 5e48 даёт 64г на 2.7e53. В одном потоке. Так что полсотни потоко-лет похоже на правду.
Поставив next строкой ниже, сразу после цикла forstep(i=sta+dd,sto,shag, получим время перебора всех паттернов без проверок вообще до 2.7e50 в 6.5ч или 0.74г до 2.7e53 или 1% от общего времени, что показывает ненужность оптимизации всех внешних циклов (при сохранении количества итераций) вплоть до проверки каждого паттерна.
-- 15.10.2025, 13:49 --PS. Чтобы убрать огрызок ETA из вывода времени, надо добавить штуки три-четыре \t в последний print:
print("Time: ",strtime(getwalltime()-t0),"\t\t\t\t").