Пентадекатлон мечты

[Yadryara]

Енто уже обсуждалось и не раз. И 6-кратный шаг и 8-этажный мат.

Прогу для D(48,20) удалось ускорить на 46% только на PARI. И была надежда, что
прогу для D(48,21) удастся ускорить ещё сильнее. Но нет, поскольку применение nu сделало старую прогу быстрее, то и ускорить её сложнее. Да и балансировка оставляет желать лучшего: я мало игрался с параметрами.

Interval         VAL
       i          nu        pqr         nu
10^5           3.8 s      4.0 s      4.1 s
10^6           7.5 s      6.8 s      6.9 s
10^7          44.9 s     38.0 s     38.1 s
10^8         422.8 s    335.3 s    316.5 s

Сравнение проводилось на высоте 1e57 для известного ранее показанного приближения с valids=18. Выигрыш пока 33% для самого большого интервала.

[EUgeneUS]

Yadryara в сообщении #1705236 писал(а):

Енто уже обсуждалось и не раз. И 6-кратный шаг и 8-этажный мат.

Обсуждаться-то, может быть и обсуждалось.
Но в текущем варианте из-за умножения на 6 (а не применения модуля 3) выкидывается половина кандидатов.

Результаты стат. анализа D(48,21).

1. Поправочные коэффициенты $b_i$ - показывают во сколько раз увеличивается вероятность найти искомое при применении шаблона и предварительной фильтрации.
Если применение шаблона и предварительной фильтрации ("большой if") гарантирует, что не возникают "лишние простые" (которые уже есть в шаблоне) ни в какой позиции, и не выполняется другой фильтрации, то $b_i$ не зависят от $N$ и места в цепочке.

Результаты:
$b_1$
теоретический: $7.599514588$
По данным Дмитрия (средний по всем позициям): $7.436374972$
По данным Евгения (средний по всем позициям): $7.553162577$

$b_3$
По данным Дмитрия (средний по всем позициям): $3.06570558$
По данным Евгения (средний по всем позициям): $2.997218379$

$b_4$
По данным Дмитрия (средний по всем позициям): $1.513787403$
По данным Евгения (средний по всем позициям): $1.484073239$

Расстраивает, что обе оценки для $b_1$ ниже теоретической
Возможно, это статистический выброс, но хорошо бы всё таки проверить правильность остатков в "большом if'е"

2. Оценки необходимого количества попыток.
Далее использовались худшие варианты оценок (из двух) для $b_i$

а) считалась вероятность $p$ найти цепочку за одну проверку в зависимости от $N$, и оценка необходимого количества проверок, как $1/p$
б) также считалось количество попыток, которые выполняются при заданном $i$, и получающиеся числа $N$ при заданном $i$
в) увеличивался порядок $i$ пока оценка количества попыток в пункте б) не превысит оценку в пункте а).

Результат 1:
1. "сошлось" при $i=10^{15}$
2. это даёт $4 \cdot 10^{14}$ кандидатов (после "большого if'а")
3. Величина $N=1.77456\cdot 10^{59}$
4. Ожидаемое количество проверок: $2.328 \cdot 10^{14}$

Чуть позже сделаю аналогичную оценку для миллиона паттернов.
То есть число кандидатов для заданного $i$ будет оцениваться как $i \cdot 0.4 \cdot 10^6$

-- 10.10.2025, 09:08 --

EUgeneUS в сообщении #1705243 писал(а):

Чуть позже сделаю аналогичную оценку для миллиона паттернов.
То есть число кандидатов для заданного $i$ будет оцениваться как $i \cdot 0.4 \cdot 10^6$

Всё таки до $300000 \approx 9!$

Результат 2:
1. "сошлось" при $i=10^{9}$
2. это даёт $1.2 \cdot 10^{14}$ кандидатов (после "большого if'а")
3. Величина $N=1.77456\cdot 10^{53}$
4. Ожидаемое количество проверок: $5.73864 \cdot 10^{13}$

Как видим:
а) ожидаемое количество проверок уменьшилось в 4 раза.
б) числа $N$ уменьшились на 6 (!) порядков. Что сильно облегчит факторизацию.
в) в каждом паттерне нужно выполнять $1.2 \cdot 10^{14}/ 300000 = 4 \cdot 10^{8}$ проверок (уже после фильтрации "большим if'ом"). Или $i=10^9$ до "большого if'а"

Минус, конечно: для каждого из 300000 нужно рассчитывать свои остатки для "большого if'а".

Тезис "нужно искать в низинах" обретает количественное выражение

[EUgeneUS]

Кстати, если для тройки фильтровать по остатку, а не умножением на шесть, то это удвоит количество кандидатов с $0.4 i$ и $0.8 i$, тогда:

1. для $i=10^{8}$
2. это даёт $2.4 \cdot 10^{13}$ кандидатов (после "большого if'а")
3. Величина $N=1.77456\cdot 10^{52}$
4. Ожидаемое количество проверок: $4.48197 \cdot 10^{13}$

То есть имеем вероятность 1/2 найти цепочку за $2.4 \cdot 10^{13}$ проверок до $N=1.77456\cdot 10^{52}$.

Можно сначала "прогнать" все $9!$ паттернов до $i=10^{8}$, а в случае неудачи - уходить дальше "в горы", до $i=10^{9}$.

-- 10.10.2025, 10:39 --

Ещё нюанс.
Финальные вероятности для $pqr$ оказались несколько больше, чем для $pqrs$.
Поэтому после всех быстрых проверок и проверок простых, нужно проверять до первой неудачи сначала все $pqrs$, а потом все $pqr$.
Это позволит "за бесплатно" поискать улучшения цепочек длиной 18-20, так как на трех крайних местах слева стоят $pqr$: если все проверки мест с 4 по 21 удачны, то проверяем третье место, если удачно, то второе, если удачно, то первое.

[Yadryara]

EUgeneUS в сообщении #1705250 писал(а):

Можно сначала "прогнать" все $9!$ паттернов до $i=10^{8}$,

Можно. И даже, пожалуй, нужно.

Когда я говорил о том, что неплохо бы если VAL будет помогать не только советами, имел в виду что будет и сам считать, причём не только по своим программам, а именно по самым быстрым.

Когда перечитывал тему, лишний раз убедился (и огорчился) в том, что и VAL и Huz считали по своим прогам, хотя программы Дмитрия были быстрее.

Паттерн из нынешней проги имеет номер:

KMK59-3-xxx-659134278

Надо ещё установить что это за xxx такой. Но мне пока лень.

И дальше, чтоб не запутаться, считать в лексикографическом порядке:

KMK59-3-xxx-123456789
KMK59-3-xxx-123456798
KMK59-3-xxx-123456879
...
KMK59-3-xxx-987654321

Где 1 — 23, 2 — 29, ..., 9 — 59.

[EUgeneUS]

Yadryara в сообщении #1705268 писал(а):

Когда перечитывал тему, лишний раз убедился (и огорчился) в том, что и VAL и Huz считали по своим прогам, хотя программы Дмитрия были быстрее.

Пока мы с ускорителями Дмитрия считали цепочки для $k=12(2n+1)$, VAL считал цепочки $k=24n$, а там простых мало, и ускорители неэффективны.
А у Хуго его pcoul - супер-пупер-мега универсальный. Он, конечно, на цепочках с большим количеством простых будет заметно медленнее, чем считать с ускорителям Дмитрия. Но против PARI\GP - даже не знаю. Было бы интересно проверить, кстати.

Yadryara в сообщении #1705268 писал(а):

И дальше, чтоб не запутаться, считать в лексикографическом порядке:

Ещё для каждого из $9!$ шаблонов нужно найти "плохие" остатки по всем простым от $3$ до $59$ для "Большого Ифа".

-- 10.10.2025, 12:34 --

И прежде чем браться за длительный расчет, нужно понять: имеющимися мощностями сможем сделать $1.2 \cdot 10^{14}$ проверок за разумное время?
Проверки "Большим Ифом" не считаются, всё что после него - считается.

Это вроде бы на два порядка меньше, чем делали при поиске пентадекатлона... Но там куча простых и ускорители...

[Yadryara]

EUgeneUS в сообщении #1705272 писал(а):

Пока мы с ускорителями Дмитрия считали цепочки для $k=12(2n+1)$, VAL считал цепочки $k=24n$, а там простых мало, и ускорители неэффективны.

Эффективны. И Дмитрий об этом прямо писал в теме. Для 3-х одиночных простых — в 6 раз быстрее.

EUgeneUS в сообщении #1705272 писал(а):

Он, конечно, на цепочках с большим количеством простых будет заметно медленнее, чем считать с ускорителям Дмитрия.

Была оценка (уже моя) что в 19 раз медленнее. И всё равно много людей считали прогой Хьюго.

EUgeneUS в сообщении #1705272 писал(а):

Но против PARI\GP - даже не знаю.

У него прога на Сях, которые обычно быстрее PARI.

EUgeneUS в сообщении #1705272 писал(а):

Было бы интересно проверить, кстати.

Вот именно. Практические тесты должны решать. Для конкретных паттернов и интервалов.

По идее надо стремиться сначала понять сколько всего паттернов для комплекта КМК59-3.

Вот нашёл для сравнения:

KMK37-11  2 * (12 + 20) * 6! = 46080

KMK59-3   2 * (.......) * 9! = ?

То есть на два-то вроде тоже надо умножать из соображений симметрии.

Я поначалу довольно неслабо путался с D(12,15). И собирал паттерны за 7 шагов.

[EUgeneUS]

Я нашел кусок логов, где считалась D(48,21) с ускорителями Дмитрия.
Паттерны там нумеруются, как "L\R-xxx", где максимальное xxx - $120$ (видимо, $6!$ перестановок брали).

Считали до

N=99907297, 12290.076s (7278.571s in PARI) per round 547e52

Это видимо, в один поток, может быть в два потока.

Правда, там паттерн, похоже был на пять простых, а не на три.

-- 10.10.2025, 14:25 --

Вот, кстати для 50000 паттернов (AFAIR, почти столько же было для D(12,15) )

1. Почти сошлось для $i=10^{9}$
2. это даёт $2 \cdot 10^{13}$ кандидатов (после "большого if'а")
3. Величина $N=1.77456\cdot 10^{53}$
4. Ожидаемое количество проверок: $5.73864 \cdot 10^{13}$

1. Надежно сошлось для $i=10^{10}$
2. это даёт $2 \cdot 10^{14}$ кандидатов (после "большого if'а")
3. Величина $N=1.77456\cdot 10^{54}$
4. Ожидаемое количество проверок: $7.31717 \cdot 10^{13}$

Так что сильно гнаться за количеством паттернов не нужно.
600 000 ($2 \cdot 9!$) - это будет прекрасно.
Но вполне можно и 50000 - 100000. Разрядность чисел на 2 порядка вырастет (плюс время на факторизацию), а ожидаемое количество проверок - около двух раз всего вырастает.

[Yadryara]

EUgeneUS в сообщении #1705288 писал(а):

Правда, там паттерн, похоже был на пять простых, а не на три.

Факторизуйте хотя бы одну находку и будет понятно.

Если уже есть программа Дмитрия, то это здорово. Может и на три (одиночных) простых тоже есть.

[EUgeneUS]

Yadryara в сообщении #1705293 писал(а):

Факторизуйте хотя бы одну находку и будет понятно.

Да на 5 простых.

С нумерацией паттернов ошибся. Была такая:
"L\Ryy-xxx", где максимальное xxx - $120$ (видимо, $6!$ перестановок брали), а максимальная yy - 24.

[Yadryara]

VAL в сообщении #1705102 писал(а):

Но я же потом растиражировал программку на 4 разных шаблона. И гонял несколько раз. И не заметил странного хвоста у nu[]?!

Не просто хвост, а две трети длины.

Потому что не надо в одиночку шарашить Мы вот только и делаем что друг за другом ошибки исправляем. Поправлю очередные.

EUgeneUS в сообщении #1705295 писал(а):

где максимальное xxx - $120$ (видимо, $6!$ перестановок брали),

Только $120 = 5!$

Yadryara в сообщении #1705236 писал(а):

Сравнение проводилось на высоте 1e57 для известного ранее показанного приближения с valids=18.

Нет, всё-таки $n$ вблизи 1e56, хотя приближение это 57-значное.

EUgeneUS в сообщении #1705250 писал(а):

Можно сначала "прогнать" все $9!$ паттернов до $i=10^{8}$, а в случае неудачи - уходить дальше "в горы", до $i=10^{9}$.

Надо посмотреть сколько каких приближений будет находиться и оценить шансы. Может лучше будет сначала посмотреть до $i=564 \cdot 10^6$. Надо ещё по времени смотреть.

[EUgeneUS]

Yadryara в сообщении #1705306 писал(а):

Надо посмотреть сколько каких приближений будет находиться и оценить шансы.

А все эти вероятности зачем считались?
Именно чтобы оценить шансы.
И они выше оценены для 1, 300000 и 50000 паттернов.
Остался вопрос: сможем ли обеспечить необходимое количество проверок за разумное время.

Желающим могу выслать "калькулятор шансов" в Экселе, и рассказать, как им пользоваться.
Только не сегодня - калькулятор остался на другом компьютере.
Кстати, шансы можно считать для любого паттерна, при следующих условиях:
1. Нужна информация для запуска сбора статистики программой из этого сообщения, а именно:
$m$, $a$, $p_1$, правильные формулы для расчета $n$ через $i$, $m$, $a$, $p_1$, а также все плохие остатки (для всех простых, которые используются в паттерне) для размещения в "Большом Ифе"
2. Статистика соберется за разумное время, за сутки, скажем.

-- 10.10.2025, 18:20 --

Yadryara в сообщении #1705284 писал(а):

Эффективны. И Дмитрий об этом прямо писал в теме. Для 3-х одиночных простых — в 6 раз быстрее.

Можно ещё такой финт провернуть:
1. Выбрать все паттерны по условию:
а) три простых
б) ноль pq
в) 13 pqr
г) 5 pqrs
д) простые в квадратах до 59 включительно.

2. Если таких паттернов будет несколько десятков (без учёта перестановок необязательных простых в квадратах), то легко можно догнать количество паттернов до нескольких десятков миллионов.
Кстати, для этого можно использовать pcoul

3. И посмотреть, что будет при таком огромном количестве паттернов.
Если количество необходимых проверок упадет на порядок (по сравнению скажем с 50000 паттернами), то выгоднее так, чем с 50000, но с ускорителями.
А величина $N$ упадёт на три порядка.

-- 10.10.2025, 18:35 --

Плюс замены $59 \leftrightarrow 61$ и $57 \leftrightarrow 61$ не сильно ухудшат качество паттерна.
Это ещё умножит количество паттернов на четыре.

Если догнать количество паттернов до $10^8$ (но хороших)
То в каждом из них можно будет проверять всего примерно $10^6$ кандидатов, прошедших "Большой Иф".

[Dmitriy40]

EUgeneUS в сообщении #1705243 писал(а):

Минус, конечно: для каждого из 300000 нужно рассчитывать свои остатки для "большого if'а".

Это мелочи. По сравнению с количество проверок по этому паттерну.

EUgeneUS в сообщении #1705250 писал(а):

Кстати, если для тройки фильтровать по остатку, а не умножением на шесть, то это удвоит количество кандидатов с $0.4 i$ и $0.8 i$,

Вот тут не понял: если по модулю 3 не отфильтровано сразу выбором p1 и m, то будет отфильтровано длинным if. Формально кандидатов вдвое больше, понятно, но реально лишняя половина кандидатов отбрасывается намного быстрее тех что проходят проверку по длинному if и проваливаются в isprime и factor/numdiv.

EUgeneUS в сообщении #1705250 писал(а):

Поэтому после всех быстрых проверок и проверок простых, нужно проверять до первой неудачи сначала все $pqrs$, а потом все $pqr$.

Если под неудачей подразумевается полная проверка мест $pqrs$, то это сильно невыгодно для больших чисел, намного лучше сразу проверить быстро как можно больше мест и если ни одно не отбросило, только тогда переходить к более сложной и долгой проверке. И тогда в каком порядке проверять $pqr$ и $pqrs$ - не вижу большой разницы, мелкая вероятно есть.

EUgeneUS в сообщении #1705272 писал(а):

И прежде чем браться за длительный расчет, нужно понять: имеющимися мощностями сможем сделать $1.2 \cdot 10^{14}$ проверок за разумное время?
Проверки "Большим Ифом" не считаются, всё что после него - считается.

Я так и не пойму это всё расчёты для поиска на чистом PARI или с ускорителями?
Если на PARI, то скорость проверок есть выше, 40с на 1e7 (на нём до факторизации не дошло), считаем 2.5e5/с, это даёт 1e5 кандидатов после длинного if (без тройки), т.е. скорость проверки после длинного if можно принять за 1e5/с. 1e14/1e5=1e9 секунд, примерно 32 года в один поток. Полсотни потоков справятся за полгода, типа. Вопрос насколько реально найти полсотни (а лучше сотню-две) потоков сроком на полгода-год.
Если же речь про счёт с ускорителями, тот тут вопросов сильно больше, начиная от времени на компиляцию и кончая тем что три проверяемых места слишком слабо ускоряются, лучше больше.
Плюс можно всё же добавить в ускорители анализ и мест $pqr,pqrs$, если на любом из них нашлось делителей до скажем $2^{15}$ больше необходимого, то кандидата отбрасывать. Так на интервале 1e6 начиная с 1e8 после if остаётся 116983 кандидата, а после такого анализа 10074, фильтрация почти 100:1. Сколько это займёт времени не знаю, надо тестировать.

[EUgeneUS]

Dmitriy40 в сообщении #1705328 писал(а):

Вот тут не понял: если по модулю 3 не отфильтровано сразу выбором p1 и m, то будет отфильтровано длинным if. Формально кандидатов вдвое больше, понятно, но реально лишняя половина кандидатов отбрасывается намного быстрее тех что проходят проверку по длинному if и проваливаются в isprime и factor/numdiv.

Понятно. С другой стороны: уменьшение количества честных кандидатов приводит к
а) росту порядка чисел, в которых нужно будет делать isprime и factor/numdiv.
Грубо: во сколько раз уменьшили число кандидатов, во столько раз выросли числа. На самом деле - несколько больше выросли, но для грубой оценки можно так считать.
б) к уменьшению вероятности найти цепочку, а значит к увеличению ожидаемого количества попыток.
Всё это можно посчитать в числах на "калькуляторе шансов". И после чего понять - что лучше.

Dmitriy40 в сообщении #1705328 писал(а):

Если под неудачей подразумевается полная проверка мест $pqrs$, то это сильно невыгодно для больших чисел, намного лучше сразу проверить быстро как можно больше мест и если ни одно не отбросило, только тогда переходить к более сложной и долгой проверке. И тогда в каком порядке проверять $pqr$ и $pqrs$ - не вижу большой разницы, мелкая вероятно есть.

Конечно, речь про проверку после всех быстрых проверок.
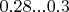
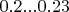
Там вероятности такие (хотя они могут исказиться после быстрых проверок): для $pqr$ - $0.28 ... 0.3$, для $pqrs$ - $0.2 ... 0.23$, то есть разница в 17-30%
И только для выбора места для первой проверки даст такой выигрыш в скорости.

Dmitriy40 в сообщении #1705328 писал(а):

Я так и не пойму это всё расчёты для поиска на чистом PARI или с ускорителями?

Будут ускорители или нет - это зависит от Вашего мнения и желания.
Все эти расчеты - для обоих вариантов. "Калькулятор шансов" - рассчитывает шансы, а не время.
Но с помощью него можно сравнить, например, в варианты:
а) 50 000 паттернов плюс ускорители
б) 10 000 000 паттернов и без ускорителей.
Но сравнить в терминах: в каком порядке $N$ вероятность найти цепочку близка к 1? Сколько для этого потребуется кандидатов? А не в терминах времени.

Dmitriy40 в сообщении #1705328 писал(а):

и кончая тем что три проверяемых места слишком слабо ускоряются, лучше больше.

Добавление простых будет уменьшать вероятность найти цепочку в 4-6 раз на каждое место.
Это приведет к росту необходимого количества проверок на порядок. А размер чисел увеличится на 1-2 порядка.
Могу сделать более точные оценки для паттернов с 4 или 5 простых.

Dmitriy40 в сообщении #1705328 писал(а):

Полсотни потоков справятся за полгода, типа. Вопрос насколько реально найти полсотни (а лучше сотню-две) потоков сроком на полгода-год.

Н-да, грустно. Напоминает басню "Лиса и виноград". Вроде бы близко, а не ухватишь

Но в любом случае нужно понять на сколько потоков можно рассчитывать.
"Господа, предлагаю делать взносы!", т.е. сообщить сколько потоков можете выделить на расчет на несколько месяцев\полгода\год.

У меня сейчас - потоков 6-7. Скорее всего, можно будет восстановить до 14-15.
Комп(ы) довольно старенькие - тактовая частота не очень высокая. Но оба поддерживают AVX.

[Yadryara]

EUgeneUS в сообщении #1705332 писал(а):

Могу сделать более точные оценки для паттернов с 4 или 5 простых.

Лучше пока с 4-мя.

EUgeneUS в сообщении #1705332 писал(а):

А не в терминах времени.

А для практического счёта нужно именно в терминах времени.

Причём на практике обнаружилась такая штука. Зависимость времени от интервала при счёте для D(48,20) была почти идеально линейной — интервал увеличиваешь в 10 раз и время во столько же раз увеличивается. А вот для D(48,21) — фиг. Да, время всё-таки становится почти линейным, но уже для весьма немаленьких интервалов. См. мою последнюю табличку выше.

Хотя ещё раз начал считать для низов.

Ну вот находки для i до 2-х миллиардов. Гарантия только, что valids не меньше 3-х по трём p, однако из-за жёсткой фильтрации находок мало и valids гораздо выше.

e50      1112222222222333333333344444444   Valids   MaxLen
         7890123456789012345678901234567
                p       p     p
203       11  1 1111  111111  1                14        6
468        1 1111  1  111 11111                14        5
3285      111 1 1 11 1  11111 1                14        5
2660      1  1 11111  1 11111 1                14        5

2202      11   11  1 111111  11                13        6
1560       11 1 1  1 11 1 11111                13        5
353        1 1111  1111 1 1  11                13        4
3432      1 1  11 1 11 111 1 11                13        3

742       1 1  11 1  11111   11                12        5
1076      1 1  11111  1 1  1 11                12        5
492       111   1111    11 1 11                12        4
3268      11   11 111  11  11 1                12        3
                                               11
                                               10
                                                9
2647         1 11 1   1 11    1                 8        2
2968        1 1 1  11   1  1  1                 8        2

EUgeneUS в сообщении #1705332 писал(а):

"Господа, предлагаю делать взносы!", т.е. сообщить сколько потоков можете выделить на расчет на несколько месяцев\полгода\год.

У меня 12 потоков и все 12 пока могу выделить.

[EUgeneUS]

Yadryara в сообщении #1705335 писал(а):

Лучше пока с 4-мя.

Для этого нужно выбрать паттерн для оценки, и предоставить по нему информацию, описанную в этом посте:

EUgeneUS в сообщении #1705308 писал(а):

Кстати, шансы можно считать для любого паттерна, при следующих условиях:

-- 11.10.2025, 09:28 --

Yadryara в сообщении #1705335 писал(а):

Причём на практике обнаружилась такая штука. Зависимость времени от интервала при счёте для D(48,20) была почти идеально линейной — интервал увеличиваешь в 10 раз и время во столько же раз увеличивается. А вот для D(48,21) — фиг

Если во время счета разрадность чисел не увеличичается, то будет линейно.
Если увеличивается, то будет расти время.
Это из-за роста времени на факторизацию и проверку простых.