Вопрос по квантовому эффекту Зенона.

[naskamejke]

Расставим некоторые точки. Я живу в мире немытых лазеров и пьющих (или непьющих) лаборантов, а не в мире КМ-туда мы ходим и КЭД-туда мы не ходим (утрирую, но не будем уточнять). И о фотонах говорю не потому, что мне это нравится (не только потому), а потому, что с ними проводят эксперименты.
Возвращаемся к этому несчастному эксперименту, с которым мне уже все ясно, насколько это вообще возможно.
Между состояниями 1 и 2 происходят осцилляции упомянутого Раби под действием RF, так что, пока не включили лазер это суперпозиция. Теперь лазер. При всей своей когерентности. Я почти ничего не знаю о лазере, но знаю, что он описывается вполне нетривиальной матрицей плотности. И вот, фотон от этого лазере, не совсем понятно когда угодил в атом. И что же, считать фазу атома после этого детерминированной? Нет уж, несогласный я

[realeugene]

naskamejke в сообщении #1704786 писал(а):

Я живу в мире немытых лазеров и пьющих (или непьющих) лаборантов, а не в мире КМ-туда мы ходим и КЭД-туда мы не ходим (утрирую, но не будем уточнять). И о фотонах говорю не потому, что мне это нравится (не только потому), а потому, что с ними проводят эксперименты.

Это замечательно, но это значит, что КТП вы всё-таки в школе должны были изучать, в отличие от меня. Я туда стараюсь не нырять потому что осознаю уровень своего незнания вопроса и его сложность. Но при этом мне известно, что главный постулат квантов: линейность всего-всего - это такая же основа КТП, как и обычных квантов.

naskamejke в сообщении #1704786 писал(а):

Я почти ничего не знаю о лазере, но знаю, что он описывается вполне нетривиальной матрицей плотности.

Ну то есть у вас исходное описание существенно стохастическое. Как раз тут не удивительно, что и на выходе всё случайно. Обычно после классического накопленного в интуиции опыта становится удивительно, когда на входе всё известно достоверно (в пределах неустранимых симметрий, конечно, вроде глобального фазового множителя), а на выходе - случайность.

naskamejke в сообщении #1704786 писал(а):

Между состояниями 1 и 2 происходят осцилляции упомянутого Раби под действием RF, так что, пока не включили лазер это суперпозиция.

Давайте не забывать, что чистое состояние осциллирует при этом только как состояние атом + фотон в резонаторе, а у атома отдельно от фотона осциллирует только матрица плотности второго ранга. Так что говорить про суперпозицию атома в этих состояниях нельзя. Но при учёте фотона в резонаторе всё осциллирует детерминированно.

Вы зря ушли от рассмотрения поляризаторов. У вас есть двумерная квантовая система. Одно ортогональное состояние портится установкой в ходе измерения и эксперимент прекращается. Зато после этого становится известно, что то, что осталось от исходно неизвестного состояния, никак не изменилось, и это состояние известно. Это пример проекции при коллапсе, не разрушающей фазу проецируемого состояния. То есть такие измерения возможны. Да и на выходе из установки Штерна-Герлаха у вас состояние разделилось на два луча с известным состоянием спина электронов в них. Только коллапс отложен до куда-то позже после проведения экспериментов с этими лучами.

-- 07.10.2025, 13:20 --

naskamejke в сообщении #1704513 писал(а):

то да вероятность распада экспоненциальна, а для малых времен линейна по времени.

Кстати, а статье по вашей ссылке как раз написано, что на малых временах и при спонтанном излучении в начальный момент времени теоретически вероятность излучения квадратична, но этот начальный интервал времени с нелинейным ростом вероятности очень короткий и его крайне сложно было бы наблюдать.

[naskamejke]

Уклоняюсь от некоторых обсуждений, да. КТП в школе не изучал, изучал после. Много осталось непонятного. Впрочем, и в КМ кое-что осталось непонятным.
Я тут, в физическом разделе заметил добрую традицию. Приходит новичек, начинает с невинного вопроса, а потом вываливает нечто космического масштаба и глупости. Так что методологически правильно относиться к новичкам соответственно. Что касается меня, насчет глупости не знаю, буду стараться. А масштаб пока таков. Проекционный постулат vs. реальность физической лаборатории. Эффект Зенона как иллюстрация.
Отбросим бОльшую часть физики и будем рассматривать стерильные "неразрушающие" измерения. Сказано, что измерение оставляет измеряемый квантовый объект в собственном состоянии измеряемой величины, и если к тому же эта величина сохраняется, то последующие измерения оставляют объект в том же состоянии. Но где сказано что-то о фазе? Состояние определено с точностью до фазы. Проектор в математическом формализме может быть определен однозначно, но кто сказал, что в реальном измерении в лаборатории не появляется неконтролируемая фаза? Предположим измерение включает активное взаимодействие с классическим прибором. Классический прибор это смесь или суперпозиция ( по-моему в данном контексте не важно) большого количества близких состояний со случайной или псевдо-случайной фазой.
В общем, не я это придумал, банальность везде описанная. В результате декогеренция, квантовый объект должен описываться матрицей плотности, потом редукция (или как-то одновременно). После всего этого мы, если захотим, можем описывать объект как чистое состояние - собственное состояние измеряемой величины, но с непонятной фазой.
Что-то я много банальностей написал. Зачем? Это я к тому, что мне кажется, если наблюдать за паром из чайника, слушать пузырьки, то на скорость закипания это не повлияет, нет активного взаимодействия прибора и объекта. А вот если все время его трогать, тогда да, повлияет. Хотя и то и то вроде как измерение.

[realeugene]

naskamejke в сообщении #1704959 писал(а):

Состояние определено с точностью до фазы.

С точностью до общей глобальной фазы. Калибровочные симметрии в электродинамике, когда можно крутить фазу поля в каждой точке - это другое. И проектор проецирует не состояние атома или фотона отдельно, а полное состояние квантовой системы. Из этого следует, что введение произвольного фазового сдвига в проектор ничего не изменяет. И проще считать, что его нет.

-- 08.10.2025, 15:35 --

naskamejke в сообщении #1704959 писал(а):

В результате декогеренция

И декогеренция - это другое.

-- 08.10.2025, 15:39 --

naskamejke в сообщении #1704959 писал(а):

Хотя и то и то вроде как измерение.

Но не квантовое

-- 08.10.2025, 16:11 --

naskamejke в сообщении #1704959 писал(а):

Классический прибор это смесь или суперпозиция ( по-моему в данном контексте не важно) большого количества близких состояний со случайной или псевдо-случайной фазой.

Внимание: вы перешли из копенгагенской интерпретации в ММИ.

Рассуждая про вопросы, по разному описываемые интерпретациями квантов, полезно не забывать, в рамках какой математики обсуждается тот или иной вопрос.

-- 08.10.2025, 16:12 --

naskamejke в сообщении #1704959 писал(а):

потом редукция (или как-то одновременно)

А вот редукции универсальной волновой функции как и случайно выбираемых проекторов в ММИ нет.

[Cos(x-pi/2)]

naskamejke в сообщении #1704959 писал(а):

<...> кто сказал, что в реальном измерении в лаборатории не появляется неконтролируемая фаза?

naskamejke, Вы в этой теме всё время беспокоитесь о некоей "фазе", но непонятно: о какой конкретно фазе и почему.

Попробуйте написать формулы для интересующих Вас измеряемых в опытах физических величин или вероятностей чего-нибудь, в которых фазовые множителеи векторов состояний влияли бы на результат. Если такого влияния не обнаружите, то, значит, и не надо беспокоиться об этих фазовых множителях.

В опытах бывают важны не сами фазы, а только разности фаз, притом только в специально поставленных опытах - интерференционного типа.

Если во время интерференционного опыта разности фаз неконтролируемо изменяются, например, быстро и хаотично, то такое нарушение когерентности будет обнаружено - наблюдаемая интерференционная картина окажется "размытой", уменьшится контрастность.

Если разности фаз изменяются достаточно медленно и регулярно (и, значит, тому есть неслучайная специальная причина), то и в этом варианте соответствующее изменение наблюдаемой интерференционной картины будет обнаружено. Это обстоятельство давно и успешно используют в технике для создания высокочувствительных приборов - интерферометров.

[naskamejke]

Хорошо. Пояснение с формулами и почему меня волнуют фазы (и какие) - для этого мне надо добраться до компьютера и книжек, чтобы покрасивее изложить.
Это несколько дней.
Как это связано с исходным вопросом (а мне кажется что связано, иначе я бы не говорил), тут мне понадобится кое-что сложить вместе, несколько дольше.
Пока тема - hold on

[naskamejke]

Уточнение про процедуру измерения. Я следую книге Садбери $\S$5.2.
Имеется объект в состоянии $\left\lvert\psi\right\rangle = \sum\limits_{}^{} c_i\left\lvert\psi_i\right\rangle$ и прибор в состоянии до измерения $\left\lvert\alpha_0\right\rangle$. После взаимодействия объекта и прибора (шредингеровская эволюция) возникнет состояние $\sum\limits_{}^{} c_i e^{i\theta_i}\left\lvert\psi_i\right\rangle\left\lvert\alpha_i\right\rangle$.Важно, что индексы у состояния прибора и объекта совпадает - в этом, собственно, смысл измерения. И появляется некая фаза. Если мы определяем состояния прибора заранее, не в связи с конкретным измерением, то эту фазу нельзя засунуть в $\left\lvert\alpha_i\right\rangle$. Доказывается, что при таком измерении статистически оператор для объекта меняется от $\left\lvert\psi\right\rangle\left\langle\psi\right\rvert$ к $\sum\limits_{}^{} \left\lvert c_i \right\rvert^2 \left\lvert\psi_i\right\rangle\left\langle\psi_i\right\rvert$.
Т. е. шредингеровская эволюция воспроизводит проекционный постулат (не доказывает, там есть нюансы, которые я опускаю).
Далее, описание классического прибора как $\left\lvert\alpha_0\right\rangle$ не точно. Нужно заменить на статистическое распределение по микроскопическим квантовым состояниям $\left\lvert\alpha_{0,s}\right\rangle$. И закон эволюции: $U(\left\lvert\psi_i\right\rangle\left\lvert\alpha_{0,s}\right\rangle) = e^{i\theta_{i,s}}\left\lvert\psi_i\right\rangle\left\lvert\alpha_{i,s}\right\rangle$. Утверждается, что для широкого класса приборов появляющаяся фаза хаотична. Индекс $i$ указывает на измеряемую величину, а индекс $s$ на множество состояний классического прибора соответствующих данному $i$. Утверждается, что проекционный постулат опять же воспроизводится.
Заметим в скобках следующее. Если описывать классический прибор как суперпозицию а не смесь, то по окончании взаимодействия состояние можно записать как $\sum\limits_{i}^{}e^{i\theta_{i,av}}\left\lvert\psi_i\right\rangle\left\lvert\alpha_{i,av}\right\rangle$, где $av$ означает некое усреднение, а фаза хаотична. В некоторых случаях это может быть важно - например разрушение интерференции в опыте Фейнмана с подсветкой для определения через какое отверстие прошел электрон, и да, конечно, важны разности фаз а не общий множитель. Но это в скобках.
А теперь к делу. Зачем мне все это мучение с Latex.
Ключевой момент - проекционный постулат воспроизводится, если измерение представляет собой активное взаимодействие прибора и объекта и если прибор обладает определенными стохастическими свойствами (хаотичность упоминаемых фаз), что собственно и определяет его классичность.
Мне это нужно было, чтобы понять эксперимент, где эффект Зенона действительно наблюдался. Измерение лазером как раз и является "правильным" измерением.
Ну а понятно, если проекционный постулат работает, то и эффект Зенона виден.
Теперь вернемся к моему исходному вопросу. Мой эксперимент можно условно описать, как "слушать пузырьки от закипающего чайника". Может быть, в конкретном эксперименте есть недостатки, но идея заключается в этом.
Я хотел бы услышать ответ, что нет, в данном типе экспериментов эффект Зенона не наблюдается, и не из-за технических нюансов, а в принципе. Потому что нет активного взаимодействия прибора и объекта. Ну, или по какой-то другой причине - в этом и вопрос. (Почитал Иванова, он пишет об измерении без взаимодействия, но там еще надо разбираться, что-то не взаимодействует, а что-то все-таки да, не хочу на это отвлекаться).
Причем отказывать моему эксперименту в праве быть "измерением" мне не хочется. То есть, мне бы хотелось думать, что в формулировке эффекта Зенона измерение может быть не любым, а четко определенного типа.
Если же это не так, если эффект Зенона в моем эксперименте действует, то давайте дадим чайники Алисе, пусть она их кипятит. Боб на некотором расстоянии слушает или не слушает пузырьки, Алиса через некоторое (относительно большое) время проверяет состояние чайников и узнает, какой чайник Боб слушал, не важно что услышал. Нехорошо это на мой взгляд.

[realeugene]

naskamejke в сообщении #1705670 писал(а):

Я следую книге Садбери

Дайте пожалуйста полную ссылку.

naskamejke в сообщении #1705670 писал(а):

Доказывается, что при таком измерении статистически оператор для объекта меняется от $\left\lvert\psi\right\rangle\left\langle\psi\right\rvert$ к $\sum\limits_{}^{} \left\lvert c_i \right\rvert^2 \left\lvert\psi_i\right\rangle\left\langle\psi_i\right\rvert$.
Т. е. шредингеровская эволюция воспроизводит проекционный постулат (не доказывает, там есть нюансы, которые я опускаю).

Но проекционный постулат - это в ЛЛ3 выражение (7,3). ЛЛ тоже рассуждают про "волновую функцию прибора", но при этом упоминают, что из-да классичности прибора он может находиться только в одном состоянии. Откуда мистическим образом следует (7,3). И никакой "случайной фазы". По вашей же формуле остаётся смесь без коллапса.

Цитата:

Это позволяет утверждать, что состояние системы прибор + электрон после измерения будет в действительности описываться не всей суммой (7,2), а лишь одним членом, соответствующим "показанию" $g_n$ прибора:

$$A_n(q)\Phi_n(\xi)$$

naskamejke в сообщении #1705670 писал(а):

И закон эволюции: $U(\left\lvert\psi_i\right\rangle\left\lvert\alpha_{0,s}\right\rangle) = e^{i\theta_{i,s}}\left\lvert\psi_i\right\rangle\left\lvert\alpha_{i,s}\right\rangle$.

Ну вот откуда берётся случайный фазовый сдвиг в унитарной эволюции? Унитарный оператор детерминирован.

У Иванова в "Как понимать квантовую механику" в разделе про проекционный постулат вообще волновая функция прибора не упоминается. Думаю, это правильно: полноценное введение волновой функции прибора требует ММИ.

Надо порыть другие учебники.

-- 13.10.2025, 09:17 --

naskamejke в сообщении #1705670 писал(а):

Я хотел бы услышать ответ, что нет, в данном типе экспериментов эффект Зенона не наблюдается, и не из-за технических нюансов, а в принципе.

Очень расплывчато понятие "данный эксперимент". На пальцах уже было сказано раньше: Зенону нужна парабола в начале распределения времени жизни исходного состояния, а тут она не заметна.

(Оффтоп)

Если вы будете вставлять пустые строки - ваш текст разобъётся на параграфы, и будет проще видеть его структуру.

[realeugene]

М. Г. Иванов, "Как понимать квантовую механику", раздел 9 - очень хороший рассказ про интерпретации. Автор выложил авторский текст своей книги в бесплатный доступ в интернете. Погуглите. Уже было второе издание. Автор - умница, рассуждает и пишет очень ясно.

Но нефизикам стоит начать с этого текста https://old.mipt.ru/students/organizati ... izikam.php

[Cos(x-pi/2)]

naskamejke в сообщении #1705670 писал(а):

Я хотел бы услышать ответ, что нет, в данном типе экспериментов эффект Зенона не наблюдается, и не из-за технических нюансов, а в принципе. Потому что нет активного взаимодействия прибора и объекта. Ну, или по какой-то другой причине - в этом и вопрос.

naskamejke

Возможно, ответ такой и будет. Ваш вопрос сложный, решаться он должен не разговорами, а количественными оценками; но не знаю, как их реально выполнить, могу только попытаться пояснить, что имею в виду.

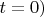
В теории нестабильных (распадающихся) квантовых систем есть математический факт: из-за ограниченности снизу спектра энергии системы вероятность системе после её приготовления (в момент времени $t=0)$ оставаться в исходном нераспавшемся состоянии убывает со временем не строго по экспоненте $e^{-t/\tau}.$ Такая экспонента это лишь аппроксимация, и применима она только в некотором интервале значений времени $t:$

$$t_1<t<t_2$$

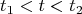
Здесь $t_1$ и $t_2$ - некие характерные значения времени для конкретной системы. При этом: $t_1\ll \tau,$ $t_2\gg\tau,$ где $\tau$ - то, что называют временем жизни нестабильного состояния.

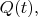
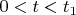
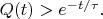
На очень малых временах, $0<t<t_1,$ распад идёт медленнее, чем любая экспонента. Т.е., если обозначить "вероятность нераспада" как $Q(t),$ то для области $0<t<t_1$ математически выводится неравенство: $Q(t)>e^{-t/\tau}.$ При $t=0$ скорость изменения вероятности нераспада вообще оказывается равной нулю: $\dot{Q}(0)=0.$

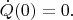
Основываясь на этом, Сударшан и Мизра в 1977 году ввели в оборот термин "квантовый эффект Зенона"; и "квантовый парадокс Зенона": мол, при непрерывном измерении нераспавшегося нестабильного состояния оно никогда не распадётся. Непрерывное измерение в вычислениях рассматривалось как предел очень большого (стремящегося к бесконечности) числа измерений над системой, каждое из которых выполняется за очень короткое время (стремящееся к нулю) одно за другим.

Но остался открытым вопрос - применимо ли представление о непрерывном измерении к реальным лабораторным наблюдениям; например, является ли трек нестабильной частицы в камере Вильсона результатом непрерывного измерения. Подобным вопросам посвящено много статей. Не все такие статьи я читал, а из прочитанного не всё показалось мне понятным; добавить ясности не смогу.

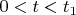
Наличие квантового эффекта Зенона долго оставалось неподтверждённым. Время $t_1$ настолько малое, что в большинстве случаев "область эффекта Зенона" $0<t<t_1$ недоступна для реальных измерений над системами. Упомянутая Вами статья Itano, Wineland и др. (doi: 10.1103/PhysRevA.41.2295) считается первой экспериментальной работой, в которой эту трудность удалось обойти так, что квантовый эффект Зенона обнаружился.

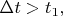
Для Вашего примера с нестабильным ядром следовало бы как-то оценить $t_1,$ а также оценить время $\Delta t,$ нужное для излучения кванта $\hbar\omega$ ядром и регистрации его приёмником. Поскольку полоса частот излучения ограничена, время $\Delta t$ не может быть сколь угодно малым. Если окажется $\Delta t>t_1,$ то эффекта Зенона в этом примере быть не должно.

Литература по квантовому эффекту Зенона обширная;

(здесь лишь некоторые ссылки)

Вот книга (хотя и старая - она написана до появления идеи о квантовом эффекте Зенона, - однако в ней подробно рассказано про неэкспоненциальность распада; см. гл. VII "Квазистационарные состояния"):

"Рассеяние, реакции и распады в нерелятивистской квантовой механике" А.И. Базь, Я.Б. Зельдович, А.М. Переломов, М. Наука, 1971. djvu-скан книги доступен на этой странице сайта EqWorld.

Две статьи в УФН (вторая так себе, её автора не воспринимаю всерьёз, но в ней есть интересные ссылки):

УФН 160, 185 (1990), Л.А. Халфин,
"Квантовый эффект Зенона"
https://ufn.ru/ru/articles/1990/10/j/

УФН 168, 1017 (1998), М.Б. Менский,
"Явление декогеренции и теория непрерывных квантовых измерений"
https://ufn.ru/ru/articles/1998/9/e/

Если статьи на английском читать можете, но не знаете, как их добывать, то попробуйте такой способ: поиском в гугле по ссылке типа "журнал, том, страница, (год)" (например, J. Math. Phys. 18, 756 (1977)) находится сайт с интересующей статьёй, там надо отыскать doi: цифровой идентификатор статьи (например, 10.1063/1.523304). Затем ввести его в окно поиска на сайте sci-hub.ru; если там в базе данных такая статья есть, то её увидите и сможете скачать. Главное, doi обнаружить; ниже в ссылках doi указываю.

Вот некоторые ранние статьи по квантовому эффекту Зенона:

J. Math. Phys. 18, 756 (1977)
The Zeno’s paradox in quantum theory
B. Misra; E. C. G. Sudarshan
doi: 10.1063/1.523304

Phys. Rev. D 16, 520 (1977)
Time evolution of unstable quantum states and a resolution of Zeno's paradox
C. B. Chiu, E. C. G. Sudarshan, B. Misra
doi: 10.1103/PhysRevD.16.520

Phys. Lett. 117 B, 34 (1982)
The time scale for the quantum zeno paradox and proton decay
C.B. Chiu, B. Misra, E.C.G. Sudarshan
doi: 10.1016/0370-2693(82)90868-1

Am. J. Phys. 48, 931 (1980)
Zeno paradox in quantum theory
A. Peres
doi: 10.1119/1.12204

Ann. Phys. 129, 33 (1980)
Nonexponential decay law
A. Peres
doi: 10.1016/0003-4916(80)90288-2

Foundations of Physics, 14, 1131 (1984)
The Classic Paradoxes of Quantum Theory
A. Peres
doi: 10.1007/BF01882494

Некоторые комментарии к эксперименту Itano с соавторами (Quantum Zeno effect, Phys. Rev. A 41, 2295 (1990), doi: 10.1103/PhysRevA.41.2295):

Phys. Lett. A 151, 109 (1990)
Quantum Zeno effect
T. Petrosky, S. Tasaki , I. Prigogine
doi: 10.1016/0375-9601(90)90173-L

Phys. Rev. A 42, 5720 (1990)
Incomplete "collapse" and partial quantum Zeno effect
A. Peres, A. Ron
doi: 10.1103/PhysRevA.42.5720


Phys. Rev. A 43, 5165 (1991)
Comment on "Quantum Zeno effect"
L. E. Ballentine
doi: 10.1103/PhysRevA.43.5165

Phys. Rev. A 43, 5168 (1991)
Reply to "Comment on ‘Quantum Zeno effect’"
W.M. Itano, D.J. Heinzen, J.J. Bollinger, D.J. Wineland
doi: 10.1103/PhysRevA.43.5168

J. Phys. A 25, 657 (1992)
A critical re-examination of the quantum Zeno paradox
D. Home, M.A.B. Whitaker
doi: 10.1088/0305-4470/25/3/022

Phys. Lett. A 173, 327 (1993)
A unified framework for quantum Zeno processes
D. Home, M.A.B. Whitaker
doi: 10.1016/0375-9601(93)90245-U

Physics Letters A 217, 203 (1996)
Understanding the quantum Zeno effect
H. Nakazato, M. Namiki, S. Pascazio, H. Rauch
doi: 10.1016/0375-9601(96)00350-7

Annals of Physics 258, 237 (1997)
A Conceptual Analysis of Quantum Zeno; Paradox, Measurement, and Experiment
D. Home, M.A.B Whitaker
doi: 10.1006/aphy.1997.5699

Пара статей на arXiv.org, там все препринты свободно доступны для скачивания:

Perspectives on the quantum Zeno paradox
W. M. Itano
https://arxiv.org/abs/quant-ph/0612187

Quantum Zeno dynamics of a field in a cavity
J-M. Raimond et al.
https://arxiv.org/abs/1207.6499

[naskamejke]

Cos(x-pi/2)
Ого! Большое спасибо за ссылки. Это мне надолго (тем более, что есть еще темы, в которых мне хотелось бы, наконец, разобраться).
То, что распад вначале не экспоненциален - это я как-то чувствовал, но в обычных учебниках эта тема уклончиво обходится.
Ну, главное, что я, кажется не одинок во вселенной с этими вопросами.

[pppppppo_98]

naskamejke в сообщении #1706092 писал(а):

То, что распад вначале не экспоненциален

он и в конце тоже неэкспотенциален - это еще труднее зафиксировать, но теория такова...

naskamejke в сообщении #1706092 писал(а):

это я как-то чувствовал, но в обычных учебниках эта тема уклончиво обходится.

в обычных приводится то что нужно для практики, и провереной практикой. Кому нужна голая теория, с туманной областью применения?

[realeugene]

realeugene в сообщении #1705726 писал(а):

М. Г. Иванов, "Как понимать квантовую механику"

Раздел 7.4 как раз посвящён квантовому эффекту Зенона.