Чтобы не ждать для каждого значения numdiv объявляем n как матрицу
n=matrix(8,33000) (в надежде что более 33000 делителей не встретится) и в цикле её обновляем просто как
n[8,numdiv((x+0)/v[1])]++ безо всяких условий.
Потом накопленную инфу уже можно анализировать как угодно, например вывести только комбинации из 1..15 простых в первой степени:
k=[2, 3, 5, 7, 11, 13, 17, 31];
for(np=1,15, print(np,": ",n[,2^np]~," : ",[round(n[j,2^np]*k[j]/(k[j]-1)) | j<-[1..#k]]); );Для паттерна
v=[4*31^3,17^3,2*3^7,5^6,2^10,3*7^3,2*11^3,13^4] и 1e4 кандидатов за минуты 4 выдаст следующее:
Код:
1: [353, 449, 596, 618, 698, 667, 665, 758] : [706, 674, 745, 721, 768, 723, 707, 783]
2: [1339, 1682, 1951, 1985, 2117, 2167, 2206, 2314] : [2678, 2523, 2439, 2316, 2329, 2348, 2344, 2391]
3: [2086, 2627, 2813, 2890, 2868, 3002, 3015, 3035] : [4172, 3941, 3516, 3372, 3155, 3252, 3203, 3136]
4: [2017, 2229, 2338, 2351, 2372, 2350, 2318, 2205] : [4034, 3344, 2923, 2743, 2609, 2546, 2463, 2279]
5: [1386, 1300, 1242, 1282, 1208, 1148, 1141, 1113] : [2772, 1950, 1553, 1496, 1329, 1244, 1212, 1150]
6: [622, 545, 453, 443, 431, 369, 407, 355] : [1244, 818, 566, 517, 474, 400, 432, 367]
7: [194, 161, 121, 110, 93, 101, 94, 77] : [388, 242, 151, 128, 102, 109, 100, 80]
8: [56, 35, 30, 16, 19, 22, 11, 17] : [112, 53, 38, 19, 21, 24, 12, 18]
9: [10, 6, 4, 8, 1, 2, 1, 3] : [20, 9, 5, 9, 1, 2, 1, 3]
10: [3, 0, 1, 0, 0, 0, 0, 0] : [6, 0, 1, 0, 0, 0, 0, 0]
11: [0, 0, 0, 0, 0, 0, 0, 0] : [0, 0, 0, 0, 0, 0, 0, 0]
12: [0, 0, 0, 0, 0, 0, 0, 0] : [0, 0, 0, 0, 0, 0, 0, 0]
13: [0, 0, 0, 0, 0, 0, 0, 0] : [0, 0, 0, 0, 0, 0, 0, 0]
14: [0, 0, 0, 0, 0, 0, 0, 0] : [0, 0, 0, 0, 0, 0, 0, 0]
15: [0, 0, 0, 0, 0, 0, 0, 0] : [0, 0, 0, 0, 0, 0, 0, 0]
Видно что более 10 простых в первых степенях не встретилось.
Для вывода например комбинаций
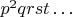
надо
2^np заменить на
3*2^np (и уменьшить предел для np до 13 чтобы не вылететь за пределы матрицы). Если подумать об этом сразу и добавить в прогу, то снова ждать не придётся, в матрице n уже всё будет накоплено.
Правда так не различить комбинации
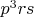
и

, т.е. наличие именно куба простого. Как и 7-й степени, и 15-й, и 31-й, и некоторые другие комбинации. Но они сильно менее вероятны и потому дают лишь мелкую поправку.
-- 07.10.2025, 12:04 --Если же таки хочется точного анализа, то объявляем вектор с желаемыми разложениями, например (указываются степени простых по убыванию):
pows=[[1], [1,1], [1,1,1], [2], [2,1], [2,1,1], [3], [3,1], [3,1,1]];Матрицу объявляем как
n=matrix(8,#pows).
В цикле команды заменяем на
f=vecsort(factor((x+7)/v[8])[,2]~,,4); j=select(t->t==f,pows,1); if(#j>0, n[6,j[1]]++);\\Будет учитывать первое совпадающее разложение
Вывод например так:
p=[31, 17, 3, 5, 2, 7, 11, 13]; foreach(Vec(vecsort(p,,1)),j, print(p[j],":\t",n[j,]); );Для предыдущего паттерна и 1e4 кандидатов и указанных выше комбинаций степеней за те же 4 минуты выведет:
Код:
2: [698, 2117, 2868, 0, 16, 42, 0, 0, 5]
3: [596, 1951, 2805, 0, 28, 96, 0, 8, 14]
5: [618, 1985, 2886, 0, 21, 64, 0, 4, 4]
7: [667, 2167, 3002, 0, 16, 50, 0, 0, 3]
11: [665, 2206, 3015, 0, 11, 30, 0, 0, 1]
13: [758, 2314, 3035, 0, 13, 23, 0, 0, 1]
17: [449, 1682, 2610, 0, 66, 193, 0, 17, 56]
31: [353, 1339, 2034, 0, 80, 338, 0, 52, 133]
Видно что ни одиночных квадратов, ни одиночных кубов нет, только вместе с простыми в первой степени, в том числе несколькими.
Что и как и зачем здесь корректировать мне думать уже лень.
-- 07.10.2025, 12:12 --И да, анализ лишь по numdiv ошибается, например для 31 и

(numdiv=8) в первом выводе указано число 2086, но в последнем видно что оно набрано как 2034+52, т.е.

и
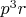
соответственно.