Объясните понятно про мощности множеств

[B3LYP]

Я слышал, что множество всех натуральных чисел является счётным, а множество всех вещественных чисел - несчётным. Я это понимаю так, что любое вещественное число можно представить как десятичную дробь с бесконечным числом знаков после запятой, отсюда и бОльшая мощность множества. То же самое можно сказать про адические числа: это как бы тоже дроби, с бесконечным числом знаков после запятой, только не слева направо, а справа налево. Всё верно?
Но мне ещё сказали, что двумерный бесконечный массив из всех натуральных чисел является счётным, а не несчётным. И это уже я совсем не понимаю. Каждый элемент такого массива - это бесконечный ряд из натуральных чисел. Т.е. вариантов даже больше, чем для вещественного числа: там каждый элемент "массива" - это число от 0 до 1, а с описанным двумерным массивом, каждый элемент - набор чисел от 1 до бесконечности. Что же такое тогда мощность множества? Или мне ерунду сказали?

[пианист]

B3LYP в сообщении #1703839 писал(а):

Всё верно?

Вроде, да.

B3LYP в сообщении #1703839 писал(а):

Каждый элемент такого массива - это бесконечный ряд из натуральных чисел

Непонятно, о чем речь, что есть "массив" - так-то это не из математики, а из айти термин. Множество бесконечных последовательностей (даже из двух элементов) несчетно.

[Dedekind]

B3LYP в сообщении #1703839 писал(а):

Но мне ещё сказали, что двумерный бесконечный массив из всех натуральных чисел является счётным, а не несчётным.

Приведите пример, что за массив?

[B3LYP]

пианист в сообщении #1703844 писал(а):

Непонятно, о чем речь, что есть "массив" - так-то это не из математики, а из айти термин. Множество бесконечных последовательностей (даже из двух элементов) несчетно.

А, ну значит просто мне неверно написали на другом форуме.
Получается что счётность это просто вроде размерности? Если "размерность" единица, то множество называется счётным, а если два или больше - то несчётным?

[Dmitriy40]

пианист
Dedekind
Очевидно имеется в виду известная перенумерация рациональных чисел. Именно как матрицы из всех комбинаций пар натуральных/целых.

B3LYP в сообщении #1703839 писал(а):

Я это понимаю так, что любое вещественное число можно представить как десятичную дробь с бесконечным числом знаков после запятой, отсюда и бОльшая мощность множества.

Не только, важно и отсутствие периода, иначе несократимые рациональные дроби тоже выражаются бесконечным числом знаков после запятой, но с периодом повторов комбинации не больше знаменателя, однако множество рациональных счётно (доказано Кантором как раз указанной Вам перенумерацией всех дробей).

[пианист]

B3LYP
Счетность это мощность множества (одна из возможных). А мощность - обобщение понятия числа элементов на бесконечные множества. Размерность это другая характеристика.

-- Вт сен 30, 2025 12:09:07 --

Dmitriy40
Может быть.

[B3LYP]

Dmitriy40 в сообщении #1703858 писал(а):

Не только, важно и отсутствие периода, иначе несократимые рациональные дроби тоже выражаются бесконечным числом знаков после запятой, но с периодом повторов комбинации не больше знаменателя, однако множество рациональных счётно (доказано Кантором как раз указанной Вам перенумерацией всех дробей).

Я не совсем понял. Почему именно несократимые?
Если мы выпишем дробь 2/3 как 0.666666..., то с одной стороны это бесконечное число знаков, но с другой стороны можно написать 0.(6), а теперь это конечное число знаков. Т.е. принцип простой: любое натуральное число можно выразить конечным числом бит, а любое вещественное число - бесконечным. Так почему, как мне написали там, мощность "двумерного множества" рациональных чисел меньше мощности множества вещественных чисел?

[wrest]

B3LYP в сообщении #1703856 писал(а):

Получается что счётность это просто вроде размерности?

Нет, счётность это такое свойство множества, при наличии которого каждому элементу можно сопоставить натуральное число ("номер" элемента) и таким образом все элементы множества можно "пересчитать".

-- 30.09.2025, 12:32 --

B3LYP в сообщении #1703883 писал(а):

Так почему, как мне написали там, мощность "двумерного множества" рациональных чисел меньше мощности множества вещественных чисел?

Вот как раз потому, что все рациональные числа (в том числе так же из "двумерного множества" рациональных чисел) можно "пересчитать", а вещественные - нет.

[Dedekind]

B3LYP в сообщении #1703883 писал(а):

Так почему, как мне написали там, мощность "двумерного множества" рациональных чисел меньше мощности множества вещественных чисел?

Потому что рациональные можно перенумеровать, а вещественные - нет. Ответ на вопрос "почему так?" - потому что так устроены рациональные и вещественные числа:)

[Dmitriy40]

B3LYP в сообщении #1703883 писал(а):

Я не совсем понял. Почему именно несократимые?

Пытался исключить целые. Бесконечные нули справа это конечно хорошо, но на мощность не влияют.

B3LYP в сообщении #1703883 писал(а):

Так почему, как мне написали там, мощность "двумерного множества" рациональных чисел меньше мощности множества вещественных чисел?

Именно потому что все рациональные числа можно перенумеровать натуральными (номером в матрице). т.е. их мощность (в некотором смысле количество) равна мощности натуральных, которых счётно.
И нет такого выражения двумерного множества рациональных чисел, это просто их все можно так записать. И размерность матрицы роли не играет, пусть хоть 100500 будет, главное придумать как все элементы перенумеровать натуральными числами. Для рациональных это возможно (Кантор показал как), для вещественных невозможно.
Конечная запись в битах это скорее следствие, ведь очевидным образом будет зависеть от метода кодирования (и системы счисления). Например число 2/3 в троичной системе счисления вполне себе конечно: $0.2_3$.

[Altenter]

B3LYP в сообщении #1703839 писал(а):

Но мне ещё сказали, что двумерный бесконечный массив из всех натуральных чисел является счётным, а не несчётным.

Скорее всего имелось ввиду, что можно пронумеровать все клетки бесконечной плоской квадратной решетки.

[B3LYP]

Dmitriy40 в сообщении #1703887 писал(а):

Для рациональных это возможно (Кантор показал как), для вещественных невозможно.

Кажется для рациональных или например натуральных это делается через "спираль"?
Скажем, чтобы переименовать все элементы двумерного множества целых чисел, выписываем спираль:
0,0
1,0
1,1
0,1
-1,1
-1,0
-1,-1
0,-1
1, -1
2,-1

Как показать, что такую спираль нельзя построить для вещественных чисел?

[mihaild]

B3LYP в сообщении #1703890 писал(а):

Как показать, что такую спираль нельзя построить для вещественных чисел?

Диагональным методом. Который для любой нумерации предъявляет непронумерованное число.

[manul91]

B3LYP

Множество из всех вещественных чисел (всех возможных бесконечных-вправо последовательностей цифр, в десятичном счислении это 0-9) - несчетно. Этих последовательностей нумеровать натуральными числами (поставить во взаимно-однозначное соответствие) - нельзя.

Множество из всех "бесконечных-вправо-и-вниз массивов" из натуральных чисел - тоже несчетно. Всех таких "массивов" нумеровать натуральными числами (поставить во взаимно-однозначное соответствие) - нельзя. Это очевидно уже потому что даже если ограничить содержимое клеток до цифр с 0 до 9, то уже первая строка одного такого "массива" - бесконечная-вправо последовательность цифр.
(одинакова ли мощность множества всех таких "массивов", с мощностью множества всех "бесконечных-вправо последовательностей цифр" т.е. вещественных чисел - уже другой вопрос.)

С другой стороны, всех клеток одного заданного "бесконечного-вправо-и-вниз массива" можно нумеровать натуральными числами (поставить во взаимно-однозначное соответствие). Например обходя их способом которого вы назвали "спиральным".

Точно также, всех разрядов одного заданного вещественного числа (одной бесконечно-вправо последовательности цифр) можно нумеровать натуральными числами (поставить во взаимно-однозначное соответствие) - тривиальным способом (у первой-слева цифры номер 1, у следующеей номер 2, и т.д.).

Похоже вы путаете две понятия: 1) возможность нумерации (т.е. счетность или несчетность) множества клеток/разрядов для одного заданного представителя класса, и 2) возможность нумерации (счетность или несчетность) множества всех представителей класса.

"Бесконечный-вправо-и-вниз массив" обычно используют для иллюстрации счетности всех рациональных чисел. Грубо говоря вписывая в каждую из его клеток соответствующую дробь из целых чисел m/n очевидным образом - то все рациональные окажутся в клеток данного массива (притом каждое рациональное будет более чем один раз - например рациональное число 0.5 из-за разных представлений 1/2, 2/4, 3/6 ... будет вписано в разных клеток). Клетки можно нумеровать, т.е. рациональные числа тоже (в данном случае нумерация даже "избыточна" - т.е. мощность рациональных чисел, не более мощности натуральных).

И лучше попытайтесь почитать сперва что-нибудь самостоятельно из учебников или хотя бы википедии про мощности множеств, а то приходится перерасказывать тривиальные вещи.

[Mihr]

B3LYP, попробуйте сначала почитать учебник.

B3LYP в сообщении #1703839 писал(а):

Но мне ещё сказали, что двумерный бесконечный массив из всех натуральных чисел является счётным, а не несчётным.

Вам сказали правильно. Если имеется в виду, что каждый элемент этого массива (натуральное число) - это и есть элемент рассматриваемого вами множества: просто элементы этого множества записаны не в бесконечную строчку, а в бесконечную таблицу. На мощности множества способ его записи не отражается.

B3LYP в сообщении #1703839 писал(а):

Каждый элемент такого массива - это бесконечный ряд из натуральных чисел.

Здесь уже под "элементом массива" вы понимаете, очевидно, его строку (либо столбец). И это тоже ни на что не влияет. Объединение (в том числе, дизъюнктное объединение) счётного множества счётных множеств также является счётным множеством. По-моему, это не более удивительно, чем равенство $0 \cdot 0=0$ либо $1 \cdot 1=1$.

B3LYP в сообщении #1703839 писал(а):

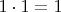
Что же такое тогда мощность множества?

Символ, который ставится в соответствие любому множеству из заданного класса равномощных множеств. То есть, чтобы понять, что такое "мощность множества", нужно сначала разобраться с вопросом, что такое "равномощные множества". Здесь как с вероятностью: чтобы привести классическое определение вероятности, сначала требуется ввести понятие равновозможных (то есть, по сути, равновероятных) событий.

B3LYP в сообщении #1703856 писал(а):

Получается что счётность это просто вроде размерности?

Не получается. Мощность - это одно, мера множества - другое, а размерность - уже третье.