B3LYPВы пронумеруйте все вещественные числа, чтобы их можно было сосчитать. А потом соберите их в матрицу, как сделано внизу. Каждый ряд матрицы - это вещественное число. Таким образом, эта матрица содержит все вещественные числа, которые можно посчитать: первое вещественное число, второе вещественное число, третье вещественное число...
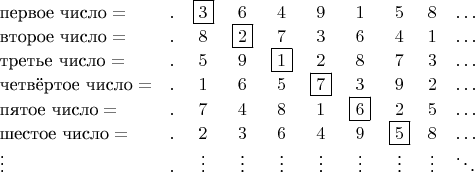
Теперь построим новое число

, используя диагональ матрицы (выделенные цифры). Для каждой позиции в числе

мы выберем цифру, которая отличается от соответствующей диагональной цифры. Например, если диагональная цифра не равна 1, мы используем 1; если она равна 1, мы используем 2.
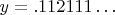
Почему число

не может находиться в нашей матрице?
*

отличается от первого числа (
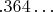
) в первой позиции:

*

отличается от второго числа (
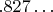
) во второй позиции:
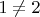
*

отличается от третьего числа (
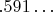
) в третьей позиции:
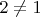
*

отличается от четвёртого числа (
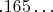
) в четвёртой позиции:
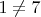
* И так далее для всех чисел в списке...
Вот противоречие: Мы предположили, что матрица содержит все вещественные числа, которые можно сосчитать. Но мы только что построили новое вещественное число

, которое гарантированно не находится в этом списке! Это означает, что невозможно сосчитать все вещественные числа - их слишком много. Множество вещественных чисел
несчётно.