SergeyGubanovВаши слова
<...> в результате в правой части уравнения движения всё равно стоит самый банальный:

осмелюсь, с извинениями за мою некомпетентность в таких делах, прокомментировать словами: этот результат ожидаемый, поскольку правая сторона линейна по касательному вектору
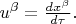
Опять же с извинениями (ещё и за то, что пытаюсь выступать как Капитан Очевидность) поясню это так. Равенство
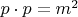
для 4-импульса частицы
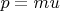
означает, какой бы хитрозаряженной частица ни была, что касательный 4-вектор

в каждой точке её мировой линии нормирован на единицу:
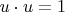
Ковариантное дифференцирование этого равенства даёт в правой стороне ноль, а в левой
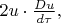
т.е.
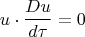
Это означает, что 4-сила
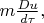
действующая на частицу из-за присутствия в пространстве-времени каких-то полей, обязана в каждой точке мировой линии "подстраиваться" под касательный вектор (он же 4-скорость частицы) так, чтобы быть ему ортогональной. Если это условие реализуется линейной зависимостью 4-силы от 4-скорости:
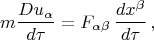
то условие ортогональности
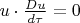
означает:
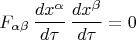
Это свёртка тензора
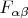
с симметричным тензором
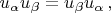
и поскольку она равна нулю, тензор
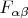
обязан быть антисимметричным:
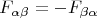
что и обеспечивается "банально" неким 4-потенциалом
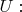
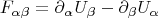
В этой схеме устройство полей и зарядов, какими бы хитрыми они ни были, обязано спрятаться в
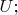
рулит не их хитрая специфика, а 4-геометрия пространства-времени.
(Ещё раз извините, если я неверно понял, о какой "банальности" у Вас шла речь, и всё слишком упростил или напутал.)