Причем здесь метатеория?
При том, что Вы заговорили об именах объектов. Имена объектов принадлежат метатеории.
Обратите также внимание на то, что любое множество имеет много имён. Если у вас
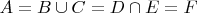
, то строки "

", "

", "
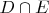
" и "

" — имена одного и того же множества. Если Вы объявили строку "

", принадлежащую метатеории, атрибутом чего-то там, то будут ли атрибутами того же самого также и строки "

", "
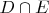
" и "

"?
Объект может быть элементом разных множеств. Имя любого такого множества тоже нужно считать атрибутом этого объекта?
Пусть отношение

задано как подмножество ДП
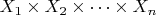
. Будем считать данное ДП универсумом

этого отношения. Тогда
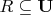
.
В дальнейшем будем называть имена множеств, из которых сформирован универсум, атрибутами этого отношения, элементы этих множеств – значениями соответствующих атрибутов, а сами множества значений – доменами этих атрибутов.
Я не понимаю, зачем нужно отказываться от стандартной терминологии теории множеств и заменять её собственными выдумками. К тому же, используя некоторые термины, которые и так используются в теории множеств, но совсем в другом смысле (например, "универсум"). Чтобы напустить тумана и запутать читателей?