Здравствуйте,
Каково среднее количество бросков монеты до выпадения 2-х орлов.
Решил задачу и у меня получилось в ответе 4 броска. Ноо я очень сомневаюсь в правильности своих рассуждений, поэтому прошу помощи:
Будем расматривать серии бросков из

подбрасываний и вероятности выпадения в конце каждой серии:

- вероятность выпадения двух орлов
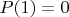
.

- вероятность выпадения двух орлов
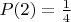
Код:
00
01
10
11

- вероятность выпадения двух орлов
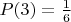
Код:
000
001
010
011
100
101
110
111
Видно, что комбинации 110 и 111 невозможны, т.к. вырадение 2-х орлов случится до совершения последнего хода, поэтому возможных комбинаций всего 6 и из них 1 благоприятная.

- вероятность выпадения двух орлов
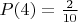
Код:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Здесь уже 6 невозможных комбинаций выпадения из всего 16, т.е. 10 возможных из которых 2 соответствуют условию.
Ну и продолжая в том же духе устанавливаем, что
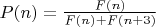
, где F(n) - n-ное число Фибоначчи. Это можно вывести строго.
Соответственно вероятность выпадения двух орлов до n бросков будет формироваться из суммы вероятностей этого события на i-том броске помноженного на вероятности не произойти на всех предыдущих.
Среднее количество бросков при котором выпадет два орла будет при таком n, при котором вероятность выпадения двух орлов будет равна

, т.е. сумма достигнет значения

или, если записать это формулой, то
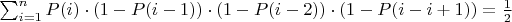
Подставляя численные значения получаем, что это условие выполняется при

т.е.
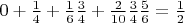
Так вот, все делалось на интуиции и есть большие сомнения в правильности моих рассуждений, в связи с чем прошу указать на ошибки и подсказать, что за величину я нашел? Будет ли это средней величиной количества бросков до выпадения 2-х орлов?
Спасибо!