Потенциальная энергия вращения

[tsapel]

В учебной литературе часто можно увидеть аналогии, проводимые для законов динамики поступательного и вращательного движения.
В частности формулы для кинетической энергии:
- поступательного движения E = $\dfrac{MV^2}{2}$, где M - масса тела, V - линейная скорость;
- вращательного движения E = $\dfrac{I\Omega^2}{2}$, где I - момент инерции тела, \Omega - скорость вращения.
А есть ли подобная аналогия для потенциальной энергии вращательного движения? Или есть ли такое понятие - потенциальная энергия вращения?

[Утундрий]

Можно ввести потенциал центробежной силы инерции. Используется, например, для вычисления формы "зеркала жидкости" при вращении какой-нибудь кастрюли.

[EUgeneUS]

Утундрий в сообщении #1701000 писал(а):

Используется, например, для вычисления формы "зеркала жидкости" при вращении какой-нибудь кастрюли.

Или при решении задачи о движении частицы в центральном поле.

[tsapel]

А вот силы, которые прикладывает студент на скамье Жуковского для изменения момента инерции, можно считать потенциальными?
Если да, то энергия, затраченная на изменение момента инерции, является потенциальной?

[realeugene]

tsapel в сообщении #1700999 писал(а):

А есть ли подобная аналогия для потенциальной энергии вращательного движения?

Нет.

И вообще, это совпадение формы - это не "аналогия", а следствие того, что кинетическая энергия квадратична по скоростям, и вы в обоих случаях выбрали координаты, в которых этот параболоид имеет наиболее простую форму.

[Утундрий]

realeugene в сообщении #1701231 писал(а):

это совпадение формы - это не "аналогия"

Отнюдь. Совпадение формы уравнений, описывающих совершенно разные явления это она самая и есть. Аналогия.

[realeugene]

Утундрий в сообщении #1701241 писал(а):

Совпадение формы уравнений, описывающих совершенно разные явления...

Явление-то совершенно одно: кинетическая энергия летящего чего-то.

[Утундрий]

(Оффтоп)

Я ему про Форму, а он мне по Ерёму...

[realeugene]

Утундрий в сообщении #1701269 писал(а):

Я ему про Форму, а он мне по Ерёму...

Не информативно.
Возможно, я не понимаю вашу слишком глубокую мысль. Или вы мою.

[DimaM]

Для системы с сохраняющимся моментом импульса можно ввести $E=L^2/(2I)$. В случае движения частицы в центральном поле это называется центробежной энергией.
Она по сути своей кинетическая, но ведет себя очень похоже на потенциальную. Особенно похоже опять же при движении частицы в центральном поле, тогда

$$E_c=\frac{L^2}{2mr^2}.$$

[madschumacher]

tsapel в сообщении #1700999 писал(а):

А есть ли подобная аналогия для потенциальной энергии вращательного движения? Или есть ли такое понятие - потенциальная энергия вращения?

Ну вообще обычно просто рассматривают вращение тела без потенциала (потенциальная энергия равна нулю). Но бывают задачи, когда возникает потенциальная энергия вращения. Например, если приложить внешнее электромагнитное поле, тогда просто добавляется энергия взаимодействия тела при помощи дипольных, квадрупольных и т.д. моментов, поляризуемостей, гиперполяризуемостей и прочего с соответствующими комбинациями электрического/магнитного поля.

[tsapel]

DimaM в сообщении #1702025 писал(а):

Для системы с сохраняющимся моментом импульса можно ввести $E=L^2/(2I)$. В случае движения частицы в центральном поле это называется центробежной энергией.
Она по сути своей кинетическая, но ведет себя очень похоже на потенциальную.

Ну да, кинетическая и есть, только вид с другого боку $E=L^2/(2I)=(I\Omega)^2/(2I)=I\Omega^2/2$.
Однако именно в системах с сохраняющимся моментом импульса потенциальная энергия не может не быть. Например студент на "скамье Жуковского", прижимая руки с гантелями к груди, совершает работу по уменьшению момента инерции. Это приводит к увеличению скорости вращения и увеличению кинетической энергии. А так как система замкнута и не обменивается энергией с внешней средой, то увеличение кинетической энергии при уменьшении момента инерции должно компенсироваться уменьшением потенциальной.

[DimaM]

tsapel в сообщении #1714862 писал(а):

А так как система замкнута и не обменивается энергией с внешней средой, то увеличение кинетической энергии при уменьшении момента инерции должно компенсироваться уменьшением потенциальной.

В данном примере кинетическая энергия увеличивается за счет работы мышц студента, то есть уменьшения запаса химической энергии. Никакой "потенциальной энергии вращения" тут нет.

[epros]

tsapel в сообщении #1714862 писал(а):

Однако именно в системах с сохраняющимся моментом импульса потенциальная энергия не может не быть.

Определитесь с тем, о какой системе отсчёта Вы говорите. Во втором сообщении темы Вам уже подсказали, что в системе с постоянной угловой скоростью вращения можно ввести потенциальную энергию центробежной силы. В системе скамьи Жуковского, которая имеет переменную угловую скорость вращения, такого не получится.

[Cos(x-pi/2)]

Вместо гантелей в руках вращающегося студента с его неизвестной химической энергией (кто его знает, чего и сколько он ел и пил?) можно рассмотреть пару грузиков на концах вращающейся пружины. Так как грузики движутся симметрично, то можно ещё упростить задачку - рассмотреть вообще всего один грузик массой $m$ на вращающемся конце невесомой пружины с жёсткостью $k.$ Другой конец пружины закреплён в идеальном шарнире в начале координат. Длина нерастянутой и несжатой пружины равна $l.$ Такая задачка наверняка есть в учебниках, но я поленился снова перечитывать книги и написал всё по-простому:

(Пояснения)

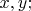
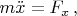
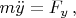
Рассмотрим всё в неподвижной системе отсчёта с декартовыми координатами грузика $x,y;$ по-школьному - с уравнениями Ньютона $m\ddot{x}=F_x\,,$ $m\ddot{y}=F_y\,,$ без лагранжиана. Энергия $E$ системы равна сумме кинетической энергии грузика и потенциальной энергии упругой деформации пружины (сжатия-растяжения, изгибов здесь нет):

$$E=\frac{m\dot{x}^2}{2}+\frac{m\dot{y}^2}{2}+\frac{1}{2}k(r-l)^2\,, \quad \text{где} \quad r=\sqrt{x^2+y^2}$$

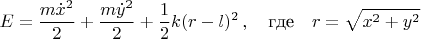
Выводится, что в замкнутой системе для решений $x(t),y(t)$ уравнений Ньютона энергия сохраняется. Значит, величина $E$ задаётся начальными значениями координат и скорости $x_0=x(0),$ $y_0=y(0),$ $\dot{x}_0=\dot{x}(0),$ $\dot{y}_0=\dot{y}(0).$

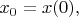
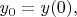
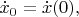
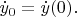
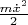
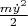
Величина энергии $E$ не изменяется с течением времени, но слагаемые в ней могут изменяться. Кинетические энергии движения грузика по осям $Ox$ и $Oy,$ т.е. величины $\frac{m\dot{x}^2}{2}$ и $\frac{m\dot{y}^2}{2}$ могут изменяться, а также если их сумма убывает, то энергия деформации пружины возрастает, и наоборот.

В выражении для $E$ выше написаны все вклады в энергию в данной задачке, никакой добавочной "энергии вращения" или добавочной потенциальной энергии не нужно.

Но эту же самую $E$ можно переписать в другом виде, притом более удобном для анализа возможных траекторий грузика.

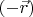
Сила $\vec{F},$ с которой пружина действует на грузик, направлена по радиус-вектору грузика $\vec{r}$ если пружина сжата, или противоположно радиус-вектору, т.е. как $(-\vec{r})$ если пружина растянута. Из этого факта выводится, что для решений уравнений Ньютона сохраняется момент импульса; в данной задачке это величина $L,$ определённая так:

$$L=m(x\dot{y}-y\dot{x})=mr^2\dot{\alpha}$$

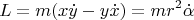
где $\alpha$ - угол между осью $Ox$ и вектором $\vec{r}.$ Проекции радиус-вектора грузика $\vec{r}$ на координатные оси это координаты грузика $x(t)$ и $y(t).$

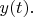
Величина $L,$ раз уж она сохраняется, задаётся начальными значениями координат и скорости грузика.

Написав производные по времени от $x=r\cos(\alpha)$ и $y=r\sin(\alpha)$ и подставив результат в формулу кинетической энергии, получим:

$$\frac{m\dot{x}^2}{2}+\frac{m\dot{y}^2}{2}\,=\,\frac{m\dot{r}^2}{2}+\frac{mr^2\dot{\alpha}^2}{2}\,=\,\frac{m\dot{r}^2}{2}+\frac{L^2}{2mr^2}$$

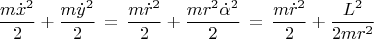
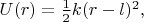
Прибавив потенциальную энергию пружины $U(r)=\frac{1}{2}k(r-l)^2,$ видим, что энергия системы $E$ запишется теперь так:

$$E\,=\,\frac{m\dot{r}^2}{2}\,+\,\frac{L^2}{2mr^2}\,+\,U(r)$$

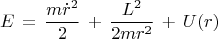
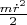
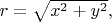
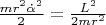
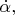
Слагаемое $\frac{m\dot{r}^2}{2}$ можно назвать кин. энергией радиального движения, так как это выражение зависит только от скорости $\dot{r}$ изменения величины радиус-вектора грузика $r=\sqrt{x^2+y^2},$ а не от скорости изменения его направления. Слагаемое $\frac{mr^2\dot{\alpha}^2}{2}=\frac{L^2}{2mr^2}$ зависит от угловой скорости $\dot{\alpha},$ с которой радиус-вектор поворачивается; это "кин. энергия вращения", её принято называть центробежной энергией.

Сумму центробежной энергии и потенциальной энергии $U(r)$ называют эффективной потенциальной энергией с заданным моментом импульса (или, жаргонно, эффективным потенциалом) $U_{eff}:$

$$U_{eff}=\frac{L^2}{2mr^2}+U(r)$$

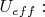
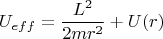
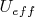
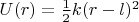
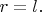
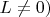
В задачах полезны графики $U_{eff}$ как функции от $r$ - такие графики помогают предсказывать возможные типы траекторий, различающиеся в зависимости от заданных $E$ и $L.$ В нашем примере график потенциальной энергии $U(r)=\frac{1}{2}k(r-l)^2$ это симметричная "потенциальная яма" - парабола с минимумом при $r=l.$ Из-за вклада ненулевой центробежной энергии (т.е. 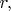при $L\neq 0)$ эффективный потенциал не симметричен - он более резко увеличивается в области малых значений $r;$ минимум эффективного потенциала находится при большем $r,$ чем минимум потенциальной энергии $U(r).$

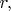
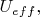
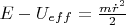
В области значений $r,$ достигаемых грузиком, уровень $E$ лежит не ниже графика $U_{eff},$ потому что разность $E-U_{eff}=\frac{m\dot{r}^2}{2}$ не может быть отрицательной.

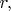
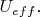
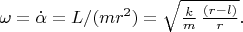
Если $E$ совпадает с минимумом эффективного потенциала, то грузику доступно единственное значение $r,$ точка минимума $U_{eff}.$ Значит, в этом случае грузик вращается по окружности с этим радиусом $r$ с постоянной круговой частотой $\omega=\dot{\alpha}=L/(mr^2)=\sqrt{\frac{k}{m}\,\frac{(r-l)}{r}}.$ При этом пружина всё время растянута, на постоянную величину $r-l>0.$

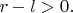
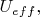
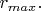
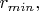
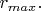
В остальных случаях есть две точки пересечения уровня $E$ с графиком $U_{eff},$ при некоторых $r_{min}$ и $r_{max}.$ Значит, в этих случаях грузик наряду с вращением (уже неравномерным, так как величина $r(t)$ в этих случаях не является постоянной) совершает некие радиальные колебания - он то приближается к началу координат на расстояние $r_{min},$ то удаляется на расстояние $r_{max}.$ Если $L=0,$ т.е. 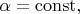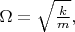$\alpha = \operatorname{const},$ то это просто гармоническое колебание груза на пружине с частотой $\Omega=\sqrt{\frac{k}{m}},$ без вращения.

Проекции вектора силы в этой задачке:

$$F_x=-\frac{\partial U}{\partial x}=-kx\,\frac{r-l}{r},\quad F_y=-\frac{\partial U}{\partial y}=-ky\,\frac{r-l}{r}$$

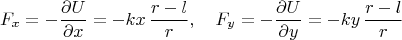
Аналитическое решение уравнений Ньютона в общем случае затрудняюсь написать, поэтому для иллюстрации всего сказанного привожу пару примеров с результатами численного расчёта траекторий. Параметры расчёта: $m=1,$ $k=1,$ $l=1$ в условных единицах.

Во вложение мне не удалось закачать zip-архив с результатами расчёта, а доступ к гугл-диску может ограничиваться у нас в РФ; поэтому поместил всё на яндекс-диск в папку с названием view: https://disk.yandex.ru/d/Ydp__Za4pXQ_NQ

Там для каждого из двух примеров с номерами 01 и 02 есть три файла: jpg с графиками, mp4 c анимацией движения грузика, и файл htm, который (если скачать все файлы себе в компьютер) при запуске в браузере позволяет увидеть всё разом - в htm для запуска видео надо кликнуть слово Play, виднеющееся над рисунками. Можно и не скачивать в компьютер, а прямо в интернете поочерёдно кликать файлы jpg и mp4. (У меня в компьютерном браузере Firefox это работает - видны и рисунки и видео; но не знаю, так ли это в других системах.)

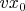
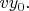
Проекции вектора начальной скорости $\dot{x}_0$ и $\dot{y}_0$ были в расчётах обозначены как $vx_0$ и $vy_0.$ Значения $E$ на графиках с эффективным потенциалом прорисовывались красным цветом в процессе расчёта траектории грузика. Вот ещё пояснения к примерам:

Пример 01_view. Начальное положение грузика было задано на оси $Ox$ в точке $x_0=1,$ т.е. в начальном состоянии пружина длиной $l=1$ не деформирована. Зато грузику придана начальная скорость $\sqrt{2}$ под углом $\pi/4$ к положению пружины. Поэтому возникло вращение, а также значительные радиальные колебания. В результате, траектория грузика сильно отличается от окружности: различие значений $r_{min}$ и $r_{max}$ очень заметное.

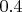
Пример 02_view. Здесь начальное положение грузика тоже выбрано на оси $Ox$ в точке $x_0=1,$ т.е. и в этом примере в начальном состоянии пружина не деформирована. Грузику придана начальная скорость $0.4$ в направлении оси $Oy,$ перпендикулярном положению пружины. В этом примере траектория грузика ближе к окружности, чем в предыдущем примере. На вставке показано начало траектории. Можно заметить, что за время одного оборота грузик совершает несколько радиальных колебаний, т.е. частота колебаний выше частоты вращения.