Оценка дисперсии тяжелохвостого закона при известном μ

[alexey007]

Как максимально точно оценить дисперсию тяжелохвостого распределения, зная точное математическое ожидание?
Проблема
У меня есть выборка из распределения с известным теоретическим средним $\mu$. Из-за длинного правого хвоста выборочное среднее $\hat\mu$ существенно смещено, а выборочная дисперсия $s^2$ недооценивает истинную дисперсию $\sigma^2$.
Что хочу
Использовать знание точного $\mu$ и саму выборку, чтобы получить более точную оценку $\sigma^2$, чем просто $s^2$.

Какие существуют статистические процедуры или ссылки на литературу, которые решают именно такую задачу: оценка дисперсии при известном $\mu$ в условиях тяжелых хвостов?

[Ghost_of_past]

alexey007 в сообщении #1699390 писал(а):

У меня есть выборка из распределения с известным теоретическим средним $\mu$.

Метод максимального правдоподобия пробовали? Правда, если распределение нетипично, то лучше, наверное, использовать какой-нибудь из методов робастного оценивания.

[dsge]

alexey007 в сообщении #1699390 писал(а):

Из-за длинного правого хвоста выборочное среднее $\hat\mu$ существенно смещено

Терминологическое замечание. Выборочное среднее является несмещенной оценкой мат.ожидания, и случайной величиной с дисперсией $\sigma^2 n^{-1}$. Так что если отличие выборочного среднего от мат.ожидания будет такого масштаба, то это нормально.

Для несмещенной выборочной дисперсии, если известно мат.ожидание, делить надо на $n$, а не $n-1$, одна степень свободы пропадает. От тяжести хвостов эти оценки никак не зависят, они справедливы для любых распределений, имеющих конечные вторые моменты.

Если известен вид распределения, то можно увеличить асимптотическую эффективность оценки (уменьшить дисперсию оценки дисперсии), используя метод максимума правдоподобия, но для этого желательно достаточно много наблюдений. Если функциональная форма плотности зависит от параметров, которые не являются мат.ожиданием и дисперсией, то эти параметры надо выразить через последние, потом дифференцировать по дисперсии при фиксированном мат ожидании. Опять, тяжесть хвостов тут ни при чем.

-- 23.08.2025, 11:56 --

Ghost_of_past в сообщении #1699400 писал(а):

Правда, если распределение нетипично, то лучше, наверное, использовать какой-нибудь из методов робастного оценивания.

Какая-то чушь в ПРР.

[Combat Zone]

dsge
Вы все правильно пишете формально. Начиная с того, что выборочное среднее не может быть смещенной оценкой, ну и прочие известные вещи.

Но ТС просто неудачно выражается, пытаясь бытовым языком описать известные эффекты и поведение выборок из распределений с тяжелыми хвостами, зачем-то задействовав при этом зарезервированный для других нужд термин.

Имелось в виду что-то такое:
В таких выборках, как у автора, выборки могут сползать вправо, в длинный хвост, что существенно повлияет на оценку выборочного среднего в данной реализации, за счет выбросов оно увеличится, порой значительно (оно совпадает с матожиданием только в среднем, т.е. и по сколь угодно большим выборкам, когда выборочное среднее рассматривается как случайная величина). Хвосты тяжелые, значит, выбросы очень вероятны. И даже если вместо выборочной дисперсии брать оценку дисперсии для случая известного матожидания $s^2_0=\frac 1n\sum_{k=1}^n(x_k-\mu)^2$, за счет наличия выбросов, значение дисперсии в некоторой реализации тоже может плохо приближать ее истинное значение, хотя она и несмещенная, эта оценка, и эффективная, и все остальное. Хотя бы один существенный выброс - квадрат становится гигантским. В общем случае, лучше этой оценки ничего нет, неприятность только в том, что матожидание не всегда известно.

Однако наш случай не общий, и один-два выброса - и эта оценка будет сильно завышена в сравнении с истинной дисперсией. Поскольку она неробастна.

При известном матожидании берут что-то вроде такого:
$\mathsf{MAD}=\mathsf{Me}(|x_1-\mu|,\ldots,|x_n-\mu|)$
$\hat\sigma = \dfrac{\mathsf{MAD}}{\Phi^{-1}(0.75)}$
и соотв., оценка дисперсии = $\hat\sigma^2$

Эта оценка робастна (т.е. устойчива к выбросам) и должна работать лучше.

Тут есть и еще одна проблема. Но я надеюсь, автор про нее знает. Распределение с тяжелыми хвостами не обязано иметь дисперсию или матожидание. Так что было бы хорошо предварительно убедиться, что вычисляя оценки, вычисляешь что-то осмысленное.

[dsge]

Combat Zone в сообщении #1699454 писал(а):

В таких выборках, как у автора, выборки могут сползать вправо, в длинный хвост, что существенно повлияет на оценку выборочного среднего в данной реализации, за счет выбросов оно увеличится, порой значительно

Надо различать тяжелые хвосты и выбросы. Тяжелые хвосты - это когда у распределения хвосты тяжелее нормального (больше вероятность, чем у нормального получить значения далекие от среднего). Если известна функциональная форма плотности и много наблюдений, то максимум правдоподобия есть самое лучшее.

Выбросы - это outliers, что-то не из нашего распределения, загрязненные данные (например, ошибка записи данных в 10 раз). Чтобы смягчить эффект этого загрязнения на оценку надо применять какую-то робастную целевую функция, растущую (или нерастущую вовсе после какого-нибудь значения аргумента) медленее квадратичной.

[Combat Zone]

Я различаю.

dsge в сообщении #1699456 писал(а):

Выбросы - это outliers, что-то не из нашего распределения, загрязненные данные

Необязательно. Это вопрос договоренностей и терминологиии.

en.wiki писал(а):

Outliers can occur by chance in any distribution, but they can indicate novel behaviour or structures in the data-set, measurement error, or that the population has a heavy-tailed distribution.

Так вот когда выбросы - не загрязненные данные, а подлинные, то вероятность их возникновения в выборке из распределения с тяжелым хвостом высока.

[dsge]

Combat Zone в сообщении #1699468 писал(а):

Так вот когда выбросы - не загрязненные данные, а подлинные, то вероятность их возникновения в выборке из распределения с тяжелым хвостом высока.

Я бы не называл то что получается из исходного распределения "выбросами". Это распределение, какое есть, оценивается МПП, если достаточно данных.
А если наблюдение отклоняется на $100\sigma$ (например, проценты не переведены в сотые по какой-то причине), то это явно выброс и никакими тяжелыми хвостами его не получить. В этом случае такое наблюдение лучше удалить и оценивать без него. Если поиск выброса невозможен (очень дорого или\и слишком много данных), то приходится делать робастные оценки, чтобы как-то смягчить искажения, смещенности.

[Combat Zone]

Ну поздно уже. Назвали, нас не спросясь. Если вам очень не нравится использовать слово выброс в таком контексте (хотя оно используется), называйте экстремальными значениями. Это не будет противоречить вашим убеждениям. Смысл тот же - все сильно съезжает, а просто удалить из выборки мы не можем, потому что это как раз подлинное значение наблюдения, ошибки нет.
А удалять без предварительного анализа нельзя ни в коем случае, вы теряете специфику распределения. На то они и тяжелые хвосты.

dsge в сообщении #1699512 писал(а):

А если наблюдение отклоняется на $100\sigma$ (например, проценты не переведены в сотые по какой-то причине), то это явно выброс и никакими тяжелыми хвостами его не получить.

У меня нет такой уверенности. А если сигма нет вообще? Все эти чудеса от анализа данных в виде ящиков с усами (оне же формулы Тьюки) рассчитаны на более-менее симметричное распределение, близкое к нормальному.
Как фильтровать выброс-ошибку от выброса, свойственного асимметричному распределению с тяжелыми хвостами - это сложный вопрос. Нам его не задавали. Нас спросили совсем другое, это мы уже увлеклись.

[dsge]

Combat Zone в сообщении #1699520 писал(а):

Ну поздно уже. Назвали, нас не спросясь.

Это авторы Википедии так назвали. Существуют не менее компетентные мнения по этому поводу.

[Combat Zone]

dsge
Называйте это как привыкли, я пойму, тут вообще речь не о том, а как оценивать дисперсию при известном матожидании. Оценка дисперсии, посчитанная традиционным образом, будет, как правило, велика.

Да, некоторые называют выбросами только "мусорные данные".

Сарказм понятен, но англовики не дураками пишется и модерируется, для справки вполне сойдет.

Не устраивает - вот классика. Это не устраивает - несите свое, более авторитетное. Хотя я при этом ничего нового не узнаю, что есть авторы, которые слово "выброс" используют в другом смысле, мне известно. Но есть и другие. Вопрос договоренностей и терминологии, повторюсь.

Цитата:

[...] above we remarked on the way in which outliers may influence the propriety of different methods of estimating parameters in the basic model. Let us consider a more specific example. Suppose the following random observations were obtained for some variable of interest:

$$1.74, 1.46, -1.28, -0.02, -0.40, 0.02, 3.89, 1.35, -0.10, 1.71$$

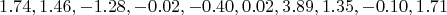
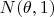
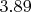
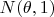
We wish to estimate the ‘centre’ of the parent population. Initial considerations suggest that the population may be normal, $ N(\theta, 1) $, so the sample mean would clearly be a sensible form of estimator. But the value $3.89$ makes us suspicious of the $N(\theta, 1)$ assumption! In fact, these data were generated as a random sample from a Cauchy distribution, with probability density function

$$f(x) = \frac{1}{\pi} (1 + x^2)^{-1}.$$

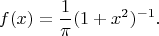
The sample mean here is not even consistent, let alone of reasonable efficiency, and we should have made very poor use of our data in the estimation procedure had we used it as an estimator of location.

Observations far removed from the main body of the sample arise naturally in sampling from a Cauchy distribution, and this contrasts with the common situation where the presence of an outlier suggests the possible inappropriateness of a model. A similar phenomenon occurs not infrequently in biological contexts. For example, the distribution of the number of cones on a fir tree for trees in a given area of forest, or the distribution of the number of lepidoptera of the same species present and observed in a particular location, are both characterized by high skewness. A typical sample from this latter type of distribution is given below; it refers to the number of individuals of a given species in a random sample of nocturnal Macrolepidoptera caught in a light-trap at Rothamsted (Fisher, Corbet and Williams, 1943):

$$11, 54, 5, 7, 4, 15, 560, 18, 120, 24, 3, 51, 3, 12, 84$$

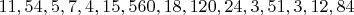
Here we have a situation in which an outlying value (the value 560) is an inherent feature of the natural data pattern, and in no way anomalous.

"Outliers in Statistical Data" by Vic Barnett and Toby Lewis

В общем-то, подход довольно понятный - не всегда ясен заранее даже вид распределения, и что-либо отсеивать, не зная природы отклонений, преждевременно. Возможно, мы при этом утратим как раз наиболее существенную информацию. А не зная этой информации, называть сильно отклоняющиеся от основной массы наблюдений значения "выбросами" в том смысле, который подразумеваете вы, и работать с ними соответственно, несколько опрометчиво. Но имеете право.

Может, хватит уже об этом? Замените слова на те, которые вам нравятся, суть у поста, к которому вы острый неприязнь испытываете, не поменяется :) А с меня не убудет. Мне неинтересен этот спор, за его бессмысленностью. Это терминологические вопросы, о них можно всегда спорить до одури, переливая из пустого в порожнее.