Возможно, Вы хотели сказать не "формулируется", а выводится.
Нет, я как раз про возможности языка. Ведь в определение формальной системы включается алфавит и правила построения формул из его символов.
Т.е. здесь:
Вся математика, которая когда-либо могла бы пригодиться в квантовой механике, наверняка формализуется в ZFC.
Вы говорили не про ZFC, а про язык исчисления предикатов первого порядка с добавлением одного бинарного предикатного символа

?
В таком-то смысле правильно, "формализовать" в таком языке действительно можно практически всю математику (за некоторыми исключениями). Но нужно иметь в виду, что это означает записать формулы для всех математических понятий, которые Вы собираетесь использовать в физической теории. И если Вы при изложении своей физической теории не собираетесь каждый раз вместо слов, обозначающих эти понятия, использовать такие трёхэтажные формулы, то Вам придётся где-то зафиксировать определения этих слов в форме: такое-то слово означает объект, удовлетворяющий такой-то формуле. Вот это и есть:
куча аксиоматики, которая определяет математические понятия, этой физической теорией используемые
Т.е. прежде чем построить формальную квантовую механику, нам придется формализовать доказательства всех теорем из стандартных курсов матанализа, линейной алгебры, диффуров, функционального анализа и всей прочей необходимой математики.
Зачем, если это уже сделано в учебниках по матанализу, линейной алгебре и т.д.? Физики обычно не этим занимаются. За исключением, разве что, когда Дирак придумывает какую-нибудь дельта-функцию, а математики потом двадцать лет ломают голову, как её корректно математически определить. Но в итоге-то строгое определение оказывается в математических учебниках, а в физических учебниках и статьях - только ссылка на него.
Так к чему я веду: раз квантовая механика существует как физическая теория, но не существует как формальная, и даже сколько-нибудь близкая к формальной, теория, может быть, эти два слова "теория" - это (шепотом) омонимы ?
Это, знаете ли, как изобретать "идеального крота" как предмет для обсуждения господ философов, намеренно не имеющего отношения к реальным кротам. Формальные системы строятся не просто для развлечения математиков, а для углублённого понимания того, как устроены любые теории, включая формулируемые на естественных языках. Ибо физикам, например, не до этого углублённого понимания, они просто строят свои теории исходя из своих интуитивных представлений о том, как устроен язык и что такое логически корректное рассуждение. А математики, которые стремятся к углублённому пониманию, уже вводят строгие определения дельта-функции или формальной системы.
Рассуждение такое. Допустим, на языке формальной системы

мы не можем сформулировать ВТФ.
Это заведомо очень бедный язык. Например, язык арифметики натуральных чисел со сложением, но без умножения, таков. Язык арифметики Пеано или язык теории множеств уже позволяет сформулировать практически что угодно. Так что этот пример физикам вряд ли интересен: в их распоряжении заведомо достаточно богатый язык, к тому же нет никаких ограничений на ввод новых слов (сопровождаемых определениями, разумеется).
Это условность. Натуральными числами можно кодировать любые утверждения о чем угодно.
Отнюдь, это буквально так: гёделевское утверждение - это утверждение о несуществовании некоего натурального числа, которое невозможно доказать в рамках данной теории, но можно доказать, если добавить аксиому о непротиворечивости данной теории. Если говорить о том, что это утверждение "кодирует", то тоже ничего интересного для физиков не вылезет. Это окажется всего лишь утверждение о несуществовании доказательства этого же утверждения.
Для физиков может быть интересно другое: теорема о неполноте - явное указание на то, что язык любой достаточно богатой теории (физической, в том числе) заведомо говорит о многих вещах, которые выходят за рамки проверяемого. Т.е. как бы нам ни хотелось, чтобы физическая теория утверждала (и отрицала) исключительно нечто проверяемое, её язык неизбежно выйдет за рамки проверяемого. И дело даже не в гёделевском утверждении о натуральных числах, в физике полно всяких глобальных утверждений типа про тепловую смерть Вселенной или про то, что всю Вселенную можно описать одной волновой функцией, которые бесконечно далеки от проверяемости. Просто так уж устроены языки: начиная утверждать какие-то обобщающие вещи, мы неизбежно где-то вылазим за рамки всех разумных обобщений.
-- Сб авг 23, 2025 13:30:52 --внутренний динамический процесс жизни баранов как-то соответствует логике нашего счёта
Нет никакой "логики счёта". Счёт (функция инкремента

) определяется не логикой, а прикладными аксиомами арифметики натуральных чисел:
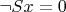
и
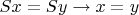
.
Фон Нейман, очевидно, какой-то смысл видел.
Возможно, что он был просто зачарован ставшими общим местом рассуждениями о том, насколько квантовая механика противоречит бытовой интуиции. Отсюда недалеко до предположения о том, что она должна противоречить общепринятой логике.
Ошибка выжившего также означает, что наблюдавшийся процесс, возможно, был важен для выживания.
А возможно, что был не важен. И никаких существенных оснований предпочесть первое второму нет. Всё говорит о том, что для выживания важно, чтобы теории соответствовали наблюдаемому. А для этого нужно просто вовремя отбрасывать теории с несоответствующей наблюдаемому прикладной аксиоматикой, но вовсе нет нужды выбирать какую-то специальную логику. Логика важна для взаимопонимания между разными людьми, но для этого она не обязана быть какой-то конкретной, она только должна быть одной и той же у разных людей, а это достигается просто путём обмена мнениями.