Философский оффтоп из темы Интерпретации квантовой механики

[Alex-Yu]

epros в сообщении #1699281 писал(а):

Alex-Yu в сообщении #1699277

писал(а):
Хм-м-м... Это мне в голову никогда не приходило. А это что, теорема такая? Или просто интуитивное суждение? Вообще какие основание такого утверждения? Не обязательно строгие. Утверждение кажется очень интересным, но хочется хоть каких-нибудь оснований.
Это стандартное определение формальной системы.

А-а-а-а-а... В этом смысле.... Формальная система это еще не теория. Не физическая теория уж точно. Оказалось, что утверждение не интересно. А жаль.

И даже чисто формально, вне физики. Не любую формальную систему можно построить на любой грамматике и правилах вывода. Из разных правил вывода получаются разные формальные системы, не эквивалентные друг другу. Так что даже формально не интересно.

[epros]

realeugene в сообщении #1699284 писал(а):

На подмножестве логики первого порядка?

На подмножестве, по без кванторов. А значит это не логика первого порядка.

epros в сообщении #1699272 писал(а):

логики предикатов для неё вообще не существует

realeugene в сообщении #1699284 писал(а):

Для коммутирующих друг с другом проекторов - почему нет?

Не знаю почему. Наверное потому что кванторы расширяют конъюнкцию и дизъюнкцию, но если конъюнкция и дизъюнкция аномальные, т.е. не соответствуют стандартным определениям, то как их расширять непонятно.

Alex-Yu в сообщении #1699304 писал(а):

Формальная система это еще не теория. Не физическая теория уж точно.

Как это не теория? Примитивно рекурсивная арифметика - вполне себе теория. Физикам, конечно такой уровень формализации неинтересен. Тем не менее, то, что они говорят, подразумевает и логические связки, и кванторы, а иногда даже кванторы второго порядка. И только поэтому их понимают не физики (которые имеют желание разобраться). Вот это и есть логика. Суть ведь не в формализации, формализация нужна только тогда, когда мы начинаем основательно докапываться до того, что именно должны обозначать те или иные слова.

Alex-Yu в сообщении #1699304 писал(а):

Не любую формальную систему можно построить на любой грамматике и правилах вывода.

Что Вы имеете в виду? Во всяком случае, формализация теории (т.е. формальная система) может быть какой угодно. Т.е. к логике она может не иметь вообще никакого отношения, вплоть до того, что в правилах вывода не будет ничего, похожего на modus ponens, а в языке не будет ничего похожего на импликацию. Это в плане формализации, а если мы захотим увидеть такую теорию на естественном языке, то, соответственно, получим множество предложений, в которых нет ничего похожего на обороты "следовательно" или "если..., то...". Вряд ли Вы вообще сходу поймёте, что это - теория.

-- Пт авг 22, 2025 11:25:21 --

realeugene в сообщении #1699284 писал(а):

Баранов в стаде всё-таки считать как-то нужно, так что стандартная арифметика нужна для моделирования мира.

Кстати, для того, чтобы считать баранов, даже примитивно рекурсивная арифметика избыточна. Достаточно элементарной арифметики, это которая без сложения и умножения. И вряд ли счётчикам баранов нужна, например, математическая индукция.

[Alex-Yu]

epros в сообщении #1699318 писал(а):

Во всяком случае, формализация теории (т.е. формальная система) может быть какой угодно.

Так. Подробнее, пожалуйста. Вы что, хотите сказать, что все формальные системы, построенные на разных (причем любых) правилах вывода, эквивалентны (имеют изоморфный набор утверждений)? Или все же эти системы разные и, вообще говоря, изоморфными быть не могут?

Речь все же изначально шла о физике. И Вы в этом контексте заявили, что правила вывода могут быть любыми. Не знаю, как иначе можно это понять, кроме как так, что законы физики могут быть формализованы в рамках любого набора правил вывода. Физиков не интересуют любые формальные системы, сами по себе формальные системы, их интересуют только такие формальные системы, в рамках которых можно описать реальные эксперименты. Причем все эксперименты в рамках одной формальной системы. А до других формальных систем нам, физикам, нет никакого дела. Они нас просто не интересуют. Если, конечно, Вы можете доказать, что все формальные системы изоморфны друг другу, тогда другое дело. Именно это было бы интересно. А то, что существуют какие-то существенно разные (т.е. не изоморфные) формальные системы... Ну пусть существуют, этот факт просто неинтересен и в обсуждаемом контексте неуместен.

[Anton_Peplov]

Разговор ушел в какие-то абстрактные выси. Предлагаю конкретизировать.

epros
Вы не могли бы проиллюстрировать Ваши идеи на примере квантовой механики, с которой началось обсуждение?

Есть несколько попыток ввести постулаты квантовой механики. На лекциях в вузе мне давали такой вариант (прошу прощения, если формулировки где-то неточны, переписывал со студенческого конспекта):

Цитата:

Первый постулат квантовой механики сопоставляет физической величине эрмитов оператор $L^2 \to L^2$. А именно: [далее следует список операторов, сопоставленных соответственно радиус-вектору, импульсу, моменту импульса и гамильтониану].

Второй постулат определяет, когда физическая величина имеет определённое значение.
Пусть система находится в состоянии $\psi$, которое является собственной функцией оператора $\hat F$. Тогда при измерении физической величины $F$ всегда будет получаться одно и то же значение, равное собственному значению $\lambda$, отвечающему собственной функции $\psi$:

$$ \hat F \psi = \lambda \psi \Rightarrow F = \lambda $$

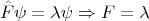Третий постулат определяет среднее значение физической величины.
Пусть система находится в состоянии $\psi$. При многократном измерении величины $F$ будут получаться некие значения, вообще говоря, разные. Однако среднее от этих значений будет равно

$$ \langle F \rangle = \int \overline \psi \hat F \psi dq $$

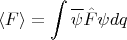
с интегрированием по всей области изменения переменных.

Как видим, в этих постулатах используются:
- математические понятия из линейной алгебры и функционального анализа
- понятия о физических величинах вообще и о радиус-векторе, импульсе, моменте импульса и гамильтониане в частности
- понятие об измерении физической величины.

Все эти понятия мы будем запихивать в аксиомы или в правила вывода? Какими аксиомами, на Ваш взгляд, нужно дополнить эти постулаты, чтобы получилась теория? Какие правила вывода будут в этой теории? Я прошу не полный список, конечно, а репрезентативную выборку примеров. В частности, какие правила вывода позволят нам записать уравнение Шрёдингера? Его аналитическое решение, когда оно удается - это часть теории или нет? Его численное решение?

Записывал ли кто-нибудь когда-нибудь квантовую механику в виде "теории", как Вы, уважаемый epros, понимаете это слово? Если да, то где, если нет, то почему?

-- 22.08.2025, 10:53 --

Alex-Yu в сообщении #1699322 писал(а):

Если, конечно, Вы можете доказать, что все формальные системы изоморфны друг другу, тогда другое дело.

Это с очевидностью не так. Даже потому, что возможность сформулировать то или иное утверждение зависит от формальной системы. Ведь в формальную систему включаются не только аксиомы и правила вывода одних утверждений из других, но и правила построения утверждений из символов алфавита. Т.е. определяющие, какие кортежи символов являются утверждениями теории (все равно, выводимыми или нет). 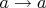Система, включающая ровно один алфавитный символ $a$, одно утверждение $a$ и одно правило вывода $a \to a$ - тоже формальная система. Полная, непротиворечивая и бесполезная.

[realeugene]

epros в сообщении #1699318 писал(а):

Наверное потому что кванторы расширяют конъюнкцию и дизъюнкцию, но если конъюнкция и дизъюнкция аномальные, т.е. не соответствуют стандартным определениям, то как их расширять непонятно.

На коммутирующих проекторах нельзя использовать стандартные конъюнкцию и дизъюнкцию?

[epros]

Alex-Yu в сообщении #1699322 писал(а):

Речь все же изначально шла о физике. И Вы в этом контексте заявили, что правила вывода могут быть любыми. Не знаю, как иначе можно это понять, кроме как так, что законы физики могут быть формализованы в рамках любого набора правил вывода. Физиков не интересуют любые формальные системы, сами по себе формальные системы, их интересуют только такие формальные системы, в рамках которых можно описать реальные эксперименты. Причем все эксперименты в рамках одной формальной системы.

Так реальная физика сложилась на фундаменте определённой логики. Мало того, помимо собственно логики в этот фундамент вошла куча разной математики. Переформулировать это всё сейчас в какой-то другой системе - это никому не нужный титанический труд. Однако я говорю о том, что этот фундамент в принципе мог бы быть совершенно другим, об этом свидетельствует существование формальных систем, не основанных на классическом исчислении предикатов. Но далее всё было бы точно так же в том смысле, что физические теории по-прежнему описывали бы реальные эксперименты, просто язык описания и правила рассуждения были бы иными. Если два таких теоретических описания (традиционное и альтернативное) разрешают или запрещают одни и те же результаты экспериментов при одних и тех же условиях, то их в этом смысле можно считать изоморфными.

Anton_Peplov в сообщении #1699323 писал(а):

Все эти понятия мы будем запихивать в аксиомы или в правила вывода?

При формализации в классическом исчислении предикатов все новые понятия определяются аксиомами. Правила вывода используются только те, которые изначально заложены в само исчисление предикатов - modus ponens и обобщения. Такой подход к формализации логики предложил Гильберт (и тому есть серьёзные основания).

Anton_Peplov в сообщении #1699323 писал(а):

Какими аксиомами, на Ваш взгляд, нужно дополнить эти постулаты, чтобы получилась теория?

Чтобы получилась физическая теория, помимо того, что определяет её собственные понятия, нужна ещё куча аксиоматики, которая определяет математические понятия, этой физической теорией используемые.

realeugene в сообщении #1699326 писал(а):

На коммутирующих проекторах нельзя использовать стандартные конъюнкцию и дизъюнкцию?

На коммутирующих проекторах получится классическая логика, с её стандартными определениями конъюнкции и дизъюнкции, а не квантовая, которая эти определения нарушает.

[Anton_Peplov]

epros в сообщении #1699345 писал(а):

Чтобы получилась физическая теория, помимо того, что определяет её собственные понятия, нужна ещё куча аксиоматики, которая определяет математические понятия, этой физической теорией используемые.

Аксиоматики, может быть, и не куча. Вся математика, которая когда-либо могла бы пригодиться в квантовой механике, наверняка формализуется в ZFC. Однако физиков в математике интересуют не аксиомы, а теоремы. И эти теоремы в формальной теории нужно доказать, прежде чем ими пользоваться. Т.е. прежде чем построить формальную квантовую механику, нам придется формализовать доказательства всех теорем из стандартных курсов матанализа, линейной алгебры, диффуров, функционального анализа и всей прочей необходимой математики. Насколько мне известно, такая работа не проделана не то что на треть, а дай Б-г чтобы процентов на десять. Только потом можно будет приступать к формализации собственно физических понятий, что тоже не фунт изюму.

Так к чему я веду: раз квантовая механика существует как физическая теория, но не существует как формальная, и даже сколько-нибудь близкая к формальной, теория, может быть, эти два слова "теория" - это (шепотом) омонимы ?

[realeugene]

epros в сообщении #1699345 писал(а):

Однако я говорю о том, что этот фундамент в принципе мог бы быть совершенно другим

Это экстраординарное утверждение требует экстраординарных доказательств. Мне всё-таки кажется, что логика была людьми не изобретена, а открыта, в ходе формирования человеческого языка. То есть она - свойство наблюдаемой реальности. А другие "фундаменты" в реальности не наблюдались.

epros в сообщении #1699345 писал(а):

На коммутирующих проекторах получится классическая логика, с её стандартными определениями конъюнкции и дизъюнкции, а не квантовая, которая эти определения нарушает.

Идея в том, что в классическом пределе из квантовой логики получается достаточно хорошее приближение классической. В которой все классические утверждения о мире определены одновременно.

[Alex-Yu]

epros в сообщении #1699345 писал(а):

Однако я говорю о том, что этот фундамент в принципе мог бы быть совершенно другим, об этом свидетельствует существование формальных систем, не основанных на классическом исчислении предикатов. Но далее всё было бы точно так же в том смысле, что физические теории по-прежнему описывали бы реальные эксперименты, просто язык описания и правила рассуждения были бы иными. Если два таких теоретических описания (традиционное и альтернативное) разрешают или запрещают одни и те же результаты экспериментов при одних и тех же условиях, то их в этом смысле можно считать изоморфными.

Вообще-то в математике обычно изоморфные объекты считаются одним и тем же объектом. Так что это та же самая формальная система, те же самые правила рассуждения и тот же самый язык (хотя, может, выраженный другими символами). Я-то, было, понял Вас так, что все формальные системы изоморфны друг другу. Т.е. фактически существует только одна формальная система (с точностью до изоморфизма). Вот это было бы интересно. Но из Ваших объяснений я понял, что это не так.

[Anton_Peplov]

Alex-Yu в сообщении #1699348 писал(а):

Вообще-то в математике обычно изоморфные объекты считаются одним и тем же объектом. Так что это та же самая формальная система, те же самые правила рассуждения и тот же самый язык (хотя, может, выраженный другими символами).

Дьявол кроется в деталях определения слова "изоморфизм".

Вот пример из топологии. На $\mathbb R$ можно ввести бесконечно много метрик, индуцирующих стандартную топологию $\mathbb R$. Человек, которого интересуют только топологические свойства пространства, может заявить, что это одно и то же топологическое пространство $\mathbb R$, но человек, которому важны расстояния, заявит, что это бесконечно много метрических пространств $(\mathbb R, \rho)$. И каждый будет прав.

Возвращаясь к баранам. Физиков интересует, какие результаты экспериментов предсказывает теория. Логиков могут интересовать более тонкие детали ее устройства. Банальный пример: теорема Геделя утверждает, что для широкого класса теорий существуют недоказуемые и неопровержимые утверждения. Допустим, в теории $A$ можно сформулировать утверждение $a$, которое не формулируется в теории $B$. Тогда с точки зрения логики это уже разные теории. Но если $a$ не доказуемо и не опровержимо в $A$, то оно не может использоваться для предсказания результатов эксперимента. А значит, для физика $A$ и $B$ могут быть одной и той же теорией.

[EminentVictorians]

realeugene в сообщении #1699347 писал(а):

Мне всё-таки кажется, что логика была людьми не изобретена, а открыта, в ходе формирования человеческого языка. То есть она - свойство наблюдаемой реальности. А другие "фундаменты" в реальности не наблюдались.

Логика же может существенно зависеть от тех объектов, к которым мы эту логику применяем. Например, пусть у вас есть база данных каких-то утверждений, которые могут "скиснуть" со временем. К таким утверждениям удобнее применять какой-нибудь вариант темпоральной логики, а не классическую (т.к. в классике истинность не меняется со временем). Если у вас есть какая-то теория в очень слабом языке, то, вероятно, у вас не останется выбора, кроме как использовать интуиционистскую логику. Еще может быть ситуация, когда у вас есть огромная база данных каких-то утверждений, в которые вы с одной стороны вроде бы верите, но без фанатизма. Эти утверждения принимаются за аксиомы. Но представьте, что эти утверждения валят огромным потоком. Они скорее всего все действительно истинные и к ним, в целом, можно относиться как к аксиомам. Но изредка новое входящее утверждение может вступить в противоречие с каким-то из той огромной кучи. Разумно использовать в такой ситуации какую-нибудь паранепротиворечивую логику.

[Alex-Yu]

Anton_Peplov в сообщении #1699350 писал(а):

Допустим, в теории $A$ можно сформулировать утверждение $a$, которое не формулируется в теории $B$.

Всегда можно факторизовать по этим отличиям. И не париться, уж коли результат один. Нет, конечно, не возбраняется заниматься фантазиями про такие отличия. Но из физики такой фантазер должен быть изгнан. Из математики -- не знаю, не моя область. Вообще интеллектуальных занятий существует много (в т.ч. и тех, которые вообще нельзя назвать наукой).

Anton_Peplov в сообщении #1699350 писал(а):

Вот пример из топологии. На $\mathbb R$ можно ввести бесконечно много метрик, индуцирующих стандартную топологию $\mathbb R$. Человек, которого интересуют только топологические свойства пространства, может заявить, что это одно и то же топологическое пространство $\mathbb R$, но человек, которому важны расстояния, заявит, что это бесконечно много метрических пространств $(\mathbb R, \rho)$. И каждый будет прав.

Расстояния измеримы. Поэтому это разные пространства, так что первый не прав. Физик не может позволить себе такую роскошь: "интересуют только топологические свойства пространства". И другие подобные роскошества. Вообще физика сложнее математики. Концептуально сложнее. Правда, математика намного сильнее развита, более обширна (именно в силу ее концептуальной простоты, относительной, конечно).

[Anton_Peplov]

Alex-Yu
Да я с Вами во всем согласен. Просто отвечал на это:

Alex-Yu в сообщении #1699348 писал(а):

Вообще-то в математике обычно изоморфные объекты считаются одним и тем же объектом.

Изоморфизм в математике, т.е. как он понимается математиками, и "изоморфизм по свойствам, интересующим физиков" - это, вообще говоря, разные вещи. И важно это понимать.

[Alex-Yu]

Anton_Peplov в сообщении #1699370 писал(а):

Изоморфизм в математике, т.е. как он понимается математиками, и "изоморфизм по свойствам, интересующим физиков" - это, вообще говоря, разные вещи.

Да, конечно. Впрочем.... Объединяем все теории, дающие одни и те же физические результаты, в один класс эквивалентности. И рассматриваем только классы эквивалентности теорий. ИМХО вполне математическая конструкция. Именно это, быть может неверно, я называю факторизацией (слово скорее из алгебры).

Загадка заключается в том, почему в класс эквивалентности физически правильных теорий (согласующихся с экспериментом) входит, в качестве представителя этого класса эквивалентности, теория построенная на основе классической логики. Меня очень давно мучает эта загадка. Вселенная слишком большая, чтобы всегда подчиняться правилам, придуманным каким-то там Аристотелем, на какой-то там планетке, на периферии заштатной галактики. Наша планетка, со всеми ее логиками, математиками, физиками и пр. -- это даже не пылинка, а что-то невообразимо более мелкое, чем пылинка. Впрочем, КМ с ее котами Шредингера, быть может, как раз "первый звоночек", свидетельствующий о том, что иногда в реальном мире классическая логика неприменима.

[Anton_Peplov]

Alex-Yu в сообщении #1699377 писал(а):

ИМХО вполне математическая конструкция.

Вряд ли. Потому что не всегда можно сказать, что проверяемо экспериментом, а что нет. Возможно, что мы еще не придумали достаточно хитроумный эксперимент. Хороший пример - неравенства Белла.