Так что аналогия всё равно не работает.
Мне интересно, как будет выглядеть ваша формула, если у нас произведение нескольких скобок, в скобках суммы разного количества слагаемых, причём, некоторые слагаемые в разных скобках могут быть одинаковые, некоторые разные… Что-нибудь типа
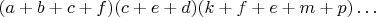
С объяснением, почему она именно такая. Интересно было бы посмотреть на ваши рассуждения.
Извините за поздний ответ.
1) Во-первых Ваш вопрос нерелевантен теме (предмету изначальной публикации). Тема посвящена возведению в степень двучлена. Возведение в степень это операция умножения величин самих на себя, а не на разные, как у Вас. Ладно ещё Вы попросили распространить соображения на возведение в степень многочлена произвольной длины, но это уже просто "не по теме".
2) Тем не менее, отвечая на Ваш вопрос "как?": да ровно также - соображения те же.
Для определения числа не приведённых слагаемых при разложении
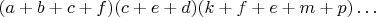
, необходимо умножение таких скобок рассматривать как размещение числа элементов равного суммарному числу членов во всех скобах (не важно повторяются ли они или нет, они и для возведения в степень скобки повторялись, это не важно), по числу мест, равному числу скобок; без повторений в рамках одной скобки и без учёта порядка.
2.1) Ну а чтобы конкретную формулу Вам предоставить, Вы должны сформулировать что означает троеточие в конце Вашего примера, с учётом того, что, как Вы словесно сформулировали, там могут быть произвольные многочлены. Формула, которую предъявил я, при этом, полагаю, любой другой не проигрывает, поскольку любая другая также с такой неопределённостью "совладать" не сможет - нужно будет больше конкретики.
Это что касается математической формулы. А словесно, Вы наверное заявите, Ваше "простое" решение сформулировать можно: "возвести в степень равную числу многочленов, число членов из всех многочленов".
Ну так и моё сформулировано словесно, только опять-таки с предоставлением понимания "что откуда берётся". То есть и тут такой подход "не проигрывает".