Но поскольку таких паттернов имеется два, я и попросил Вас уточнить, о каком идёт речь.
Мой тест не отвечает на вопрос: "где?" Он только дает ответ: "возможно/не возможно".
Если ответ "возможно" - раслывчатый, то ответ "не возможно" - категорический.
Допустим, если проверив тестом числа до какого-то достаточно большого примоиала, например

и не найти

подряд идущих взамно простых чисел на интервале натуральных чисел длиной
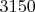
, то ответ "не возможно" даст категорический ответ на всю гипотезу, т.к если нет у взаимно простых, то и у простых чисел не будет. Ибо первые - это потенциальные кандидаты во вторые. Дальше от этого примориала все будет только хуже.