Например, последовательность разностей двух соседних простых чисел
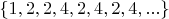
, возьмем любой отрезок из этой последовательности, как часто этот отрезок будет повторятся,
Такой отрезок называется паттерном, а удовлетворяющий ему отрезок натурального ряда — кортежем. И кортежных тем на форуме уже полным-полно. Если хотите, приходите в такую тему, а здесь это вроде бы оффтоп.
Сравнительно недавно — около полугода назад очень подробно объясняли человеку, как искать такие кортежи.
И можно ли встретить любую (вероятную, так как 2, 2 всречается только один раз
Паттерн, кортежей по которому ожидается бесконечное количество называется допустимым. Это гипотеза Диксона.
как часто этот отрезок будет повторятся,
Об этом говорит гипотеза HL1 и мы научились считать по ней, но не для всех паттернов, а только для довольно небольших длин и диаметров. Как раз недавно был обсчитан паттерн длиной 21 и диаметром 420.
существует бесконечно много пар простых на расстоянии не больше

(т.е. хотя бы какая-то разность, не большая этого числа, встречается бесконечно много раз).
Насколько понимаю,
не меньшая этого числа. То есть и гэп 248, и гэп 250 встречаются бесконечно много раз.