По идее, раз мы сделали неравносильный переход, то должны корни подставить и проверить, что в нашем случае практически невозможно.
Необязательно. Вам достаточно проверить, что уравнение кроме
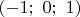
имеет ещё хотя бы один корень (это будет означать, что оно имеет ровно пять корней — все те, что вы и нашли). Это можно сделать, показав, что
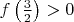
и
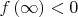
, где
![$f(x)=\sqrt[3]{x-1}+\sqrt[3]{x+1}-x\sqrt[3]{2}$ $f(x)=\sqrt[3]{x-1}+\sqrt[3]{x+1}-x\sqrt[3]{2}$](https://dxdy-01.korotkov.co.uk/f/4/3/c/43cbcb3bd701fb56ff660bf0a3ce3b0882.png)
.
Но, конечно же, задачу лучше решать так: