Можно ли построить логику с помощью школьной математики?

[BorisK]

В общем, при доказательстве я прозевал случай, когда $I(\varphi) \subseteq I(\psi)$ не выполняется, но при этом $I(\varphi) \cap I(\psi) \ne \varnothing$ и $I(\psi) \ne I(\forall x (\psi))$.
А вот и пример, опровергающий то, что $BF$ тавтология для универсума $\{a,b,c\} \times \{a,b,c\}$.
Пример: $I(\varphi) = [\ast~~\{a,b\}]$; $ I(\psi) = [\{b\}~~\{a,b\}]$.
Можно еще немало подобных примеров придумать.
Поспешил – людей насмешил! Это про меня.
Зато проблема решена!

[epros]

BorisK в сообщении #1694341 писал(а):

Формула $0=0$ не есть выражение на языке первого порядка.

Про синтаксис первого порядка Вам всё ещё нужно почитать повнимательнее.

[BorisK]

Сейчас я могу сформулировать точные условия, при которых $BF$ не общезначима. Это равносильно тому, что формула $\varphi \wedge \psi \wedge \neg (\forall x~\psi)$ выполнима.
В интерпретации это означает, что $I(BF)$ не равна универсуму равносильно тому, что не подтверждается соотношение $(I(\varphi) \cap I(\psi)) \subseteq I(\forall x~\psi)$. Это условие, как мне представляется, облегчает поиск опровергающей интерпретации. Ему же соответствует приведенный выше пример, поскольку для него $I(\varphi) \cap I(\psi) = [\{a\}~~\{a,b\}]$, а $I(\forall x~\psi) = \varnothing$.

[epros]

BorisK в сообщении #1694397 писал(а):

Это равносильно тому, что формула $\varphi \wedge \psi \wedge \neg (\forall x~\psi)$ выполнима.

Нетрудно получить эквивалентными преобразованиями в булевой алгебре, что Ваша формула эквивалентна $(\forall x~\neg \varphi) \lor (\forall x~\neg \psi) \lor (\forall x~\psi)$. Это значит, что её нарушит любой пример, в котором $(\exists x~\varphi) \land (\exists x~\psi) \land (\exists x~\neg \psi)$.

Прочие пляски с бубном ни к чему.

[BorisK]

epros в сообщении #1694402 писал(а):

Прочие пляски с бубном ни к чему.

А мне подходят эти пляски. И, надеюсь, они походят не только для меня.
В прошлом моем сообщении опечатка. Вместо $(I(\varphi) \cap I(\psi)) = [\{a\}~~\{a,b\}]$ надо читать $(I(\varphi) \cap I(\psi)) = [\{b\}~~\{a,b\}]$.

[epros]

BorisK в сообщении #1694403 писал(а):

А мне подходят эти пляски.

Они мешают Вам сразу увидеть, когда вместо кванторов всеобщности появляются кванторы существования.

[BorisK]

epros в сообщении #1694402 писал(а):

Нетрудно получить эквивалентными преобразованиями в булевой алгебре, что Ваша формула эквивалентна $(\forall x~\neg \varphi) \lor (\forall x~\neg \psi) \lor (\forall x~\psi)$.

Из этого следует, что формула $\neg \psi = \forall x~\neg \psi$. Поясните, пожалуйста, как это возможно в общем случае, если для $\psi$, в отличие от $\varphi$, не задано никаких условий?
Взять хотя бы пример $I(\psi) = [\{b\}~~\{a,b\}]$. Для него невозможно подтвердить равенство $\neg \psi = \forall x~\neg \psi$.

-- 16.07.2025, 10:48 --

[epros]

BorisK в сообщении #1694408 писал(а):

epros в сообщении #1694402 писал(а):

Нетрудно получить эквивалентными преобразованиями в булевой алгебре, что Ваша формула эквивалентна $(\forall x~\neg \varphi) \lor (\forall x~\neg \psi) \lor (\forall x~\psi)$.

Из этого следует, что формула $\neg \psi = \forall x~\neg \psi$.

Я не понимаю о чём это. Что это за синтаксис? В синтаксисе первого порядка предикатные символ $=$ применяется только к термам, а не к формулам.

В булевой алгебре импликация $A \to B$ эквивалентна $\neg A \lor B$. Переписываете Вашу формулу в таком виде, раскрываете скобки, потом применяете правило обобщения ко всей формуле в целом и получаете то, что записано в приведённой Вами цитате.

-- Ср июл 16, 2025 13:05:18 --

Ага, догадался. Равенство Вы употребили там, где должна быть равносильность?

Да, $\neg \psi$ равносильно $\forall x~\neg \psi$: В одну сторону оно следует в силу правила обобщения, а в другую сторону оно следует в силу схемы аксиом конкретизации всеобщности.

[dgwuqtj]

epros в сообщении #1694416 писал(а):

Да, $\neg \psi$ равносильно $\forall x~\neg \psi$: В одну сторону оно следует в силу правила обобщения, а в другую сторону оно следует в силу схемы аксиом конкретизации всеобщности.

Равносильно в том смысле, что они друг из друга выводятся. При этом $\neg \psi \leftrightarrow \forall x \, \neg \psi$ не общезначима.

[BorisK]

dgwuqtj в сообщении #1694438 писал(а):

Равносильно в том смысле, что они друг из друга выводятся. При этом $\neg \psi \leftrightarrow \forall x \, \neg \psi$ не общезначима.

Согласен с dgwuqtj.
Здесь тот случай, когда правило обобщения для формулы $\psi$ работает не для вех возможных случаев. Равносильность также означает, что $\neg \psi$ и $\forall x \, \neg \psi$ содержат один и тот же состав выполняющих подстановок во всех интерпретациях. А это, как я показал ранее, не так.

[epros]

BorisK в сообщении #1694443 писал(а):

Равносильность также означает, что $\neg \psi$ и $\forall x \, \neg \psi$ содержат один и тот же состав выполняющих подстановок во всех интерпретациях. А это, как я показал ранее, не так.

Уточнение dgwuqtj абсолютно верно, формула равносильности - не тавтология. Но если некая заданная $\psi$ является аксиомой (или выводимым утверждением) рассматриваемой теории (например, упоминавшаяся формула $x \times 0=0$ является аксиомой арифметики Пеано), то во всех моделях этой теории истинны как формула без квантора, так и формула с квантором всеобщности.

Суть тут не в интерпретациях, а в том, что правило обобщения имеет ограничения на применение. На применение его к выводимому утверждению теории (или к аксиоме) ограничений нет.

[BorisK]

В рамках данной темы предлагаю обсудить следующий вопрос. В математике есть немало положений, которые принимаются без доказательств и становятся «незыблемыми» лишь потому, что их принимает большинство математиков. Есть и такие положения, которые ведут к «утрате определенности» в математике. К ним, в частности, относится правило обобщения ($Gen$):
$(\forall x_i)B$ follows from $B$ (E. Mendelson),
которое принимается без всяких ограничений.
В результате получается, что в исчислении предикатов перестает быть безусловно правильной теорема дедукции ($DT$), в частности, правило $\frac {B}{\forall xB}$ не означает, что формула $B \to \forall x~B$ тавтология. Причем, как это ранее было показано, можно предложить бесчисленное множество примеров не соблюдения теоремы дедукции для данного правила.
А почему бы в исчислении предикатов не предложить (хотя бы как вариант на первых порах) другую формулировку правило обобщения?
Например, такую
$GenDT$: $\frac {B}{\forall x~B}$ при условии, что в $B$ нет свободных вхождений переменной $x$.
Тогда мы получили бы вариант исчисления предикатов, в котором не нарушалась бы теорема дедукции.
В натуральном выводе, кстати, $GenDT$ так и формулируется, только часто называется иначе.

[epros]

BorisK, это правильная тема: обсудить, почему в исчислении предикатов берётся такая аксиоматика, а не другая, в частности, зачем нужно именно такое правило обобщения, а не другое. Ранее я задавал Вам вопрос:

epros в сообщении #1694174 писал(а):

А Вам понятно, почему в аксиоматике логики первого порядка должна быть схема аксиом $\bigl(\forall x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to \psi\bigr)$, где $\psi$ не имеет свободных вхождений $x$?

У Вас есть мысли на этот счёт?

BorisK в сообщении #1694578 писал(а):

получается, что в исчислении предикатов перестает быть безусловно правильной теорема дедукции ($DT$), в частности, правило $\frac {B}{\forall xB}$ не означает, что формула $B \to \forall x~B$ тавтология.

Это неточность: теорема дедукции остаётся безусловно правильной. Но вот применение правила обобщения ограничено именно в рамках дедукции.

BorisK в сообщении #1694578 писал(а):

А почему бы в исчислении предикатов не предложить (хотя бы как вариант на первых порах) другую формулировку правило обобщения?
Например, такую
$GenDT$: $\frac {B}{\forall x~B}$ при условии, что в $B$ нет свободных вхождений переменной $x$.

Потому что такое обобщение не имеет смысла. Попробуйте ответить на первый мой вопрос. После этого можно будет обсудить, зачем нам вообще нужно правило обобщения.

[dgwuqtj]

BorisK
Речь идёт просто про какую-то логику или про такую, которая позволяет формализацию хотя бы части математики? Во втором случае нужны синтаксис, правила вывода и модели (интерпретации). Причём должны выполняться теорема о корректности вывода и теорема о полноте вывода. Для классической логики и теоретико-множественных моделей это так (хоть для исчисления предикатов по Гильберту, хоть для естественного вывода, хоть для исчисления секвенций). Для многих других логик и подходящих моделей это тоже работает, включая даже те логики, которые не покрываются классической. Всякие там теоремы о дедукции или об устранении сечений — это уже приятные бонусы, но вообще вывод может даже не быть конструктивным.

Если вы придумали новый класс моделей для логики и хотите модифицировать вывод, вам придётся заново доказывать эти две теоремы.

[BorisK]

epros в сообщении #1694582 писал(а):

Это неточность: теорема дедукции остаётся безусловно правильной. Но вот применение правила обобщения ограничено именно в рамках дедукции.

С замечанием согласен двумя руками .

Цитата:

Ранее я задавал Вам вопрос:

epros в сообщении #1694174 писал(а):

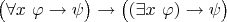
А Вам понятно, почему в аксиоматике логики первого порядка должна быть схема аксиом $\bigl(\forall x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to \psi\bigr)$, где $\psi$ не имеет свободных вхождений $x$?

У Вас есть мысли на этот счёт?

Насколько я знаю, подобная формула выведена в исчислении предикатов № 9 в списке, хотя я не знаю, как она выведена. У меня практически нет мыслей по этому поводу, так как мне пока что трудно представить, как сформулированную Вами схему аксиом можно использовать.

Цитата:

Потому что такое обобщение не имеет смысла. Попробуйте ответить на первый мой вопрос. После этого можно будет обсудить, зачем нам вообще нужно правило обобщения.

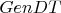
На первый вопрос я ответа не знаю (см. выше). А вот по поводу «такое обобщение не имеет смысла» не согласен. Интерпретация $GenDT$ позволяет существенно расширить область применения операций и проверок включения для многоместных отношений, которые можно использовать в качестве интерпретации многоместных предикатов.

dgwuqtj в сообщении #1694584 писал(а):

Если вы придумали новый класс моделей для логики и хотите модифицировать вывод, вам придётся заново доказывать эти две теоремы.

Представьте себе алгебраическую систему, в которой вместо доказательства тавтологичности формулы используются доказательства равенства соответствующих выражений и структур универсуму, и доказано утверждение, согласно которому операции, соответствующие логическим связкам, и проверки соотношений выполняются для всех объектов носителя. А этими объектами являются многоместные отношения, которые можно использовать в качестве интерпретаций многоместных предикатов. Такой алгебраической системой я занимаюсь. Так что эти две теоремы тут, как мне представляется, присутствуют.