Если бы мы пожелали привести (1.1) к виду с коэффициентами при кубах:

;
Оказалось бы, что для компенсации величины:
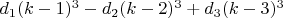
Число
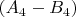
также должно стать коэффициентом

.
Сходу замечание: фразы типа "если бы мы пожелали привести" недопустимы в строгих математических рассуждениях и за ними чаще всего кроется ошибка. Потому что из того, что не сработает какое-то наше "пожелание", какой-то наш
план получения какого-то равенства,
не следует, что это равенство вообще не справедливо. Может, оно справедливо, просто наш план его получения не работает.
Теперь подробнее. До этой фразы Вы получили два равенства:
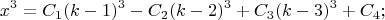
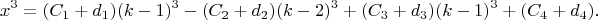
Последнее равенство - это (1.1) с подставленными туда выражениями (1.2).
Если бы Вы откуда-то знали, что
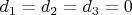
, то Вы действительно смогли бы вывести отсюда
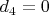
и, значит,
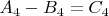
, как Вы и утверждаете.
Но может быть, все

ненулевые (причём они могут быть как положительными, так и отрицательными)? Опровержения этого у Вас нет.
Вероятно, Вы не понимаете одного момента: если одно выражение не приводится к другому алгебраическими преобразованиями, то это не значит, что эти выражения не равны. Если получилось привести одну формулу к другой - значит они равны, а если не получилось - значит непонятно: может равны (при каких-то значениях переменных), может нет.
Простейшая иллюстрация: Вы никак алгебраически не приведёте
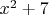
к виду

. Значит ли это, что
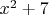
не может быть равно

? Да нет, при

они равны.
Вот такие фразы тоже непонятно как перевести на строгий математический язык (и без формул не понять, о чём тут вообще речь):
потому что кубы в скобках правой части (3) могут появиться лишь в связке со свободным членом, и в тоже время, само предъявленное разложение кубов, возможно лишь при тех же свободных членах за скобками правых частей (3).