Тут мы еще не до конца нашли все равновесия в исходной игре.
Исходная игра.
1.

- вероятность, что при паре

Алиса покажет

. Не будем накладывать на неё никаких ограничений, кроме того что это - вероятность:
![$p_{xy} \in [0,1]$ $p_{xy} \in [0,1]$](https://dxdy-01.korotkov.co.uk/f/8/0/e/80ed7cc490199ebb7ed7bb8a8ce8361f82.png)
2.
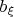
- вероятность того, что Боб скажет "показано бОльшее", при условии, что он видит

3. Введем "расширенную стратегию Боба"
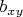
- вероятность того, то Боб скажет "показано

(число из ГСЧ номер 1)", при условии что Алисе выпала пара

Строится она так
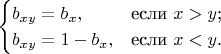
4. Теперь в каждой точке

выигрыш Алисы:
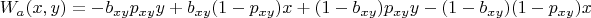
После перегруппировке слагаемых:
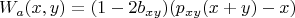
5. Легко видеть, что
а) если
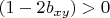
, то Алиса выбирает
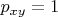
, и выигрывает в этой точке

б) если
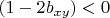
, то Алиса выбирает
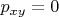
, и выигрывает в этой точке

6. Суммарный выигрыш Алисы положительный для любой нетривиальной стратегии Боба.
А значит у Боба одна равновесная стратегия, тривиальная:
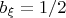
почти всюду.
Ч.Т.Д.