Здравствуйте,
nnosipovУ меня сложилось впечатление, что нельзя решать такие уравнения с помощью Vieta jumping, если старшие коеффициент не равны

, но тут кажется можно.
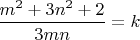
Для начала заметим, что

, так как
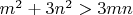
. Для любого

ищем наименьшее решение в нат. числах.
Допустим, что для фиксиранного

наименьшее решение
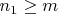
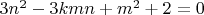
Заметим, что если

- решение, то и
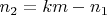
тоже целое, да еще и положительное и
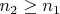
. Тогда
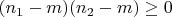
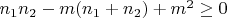
Формулы Виета
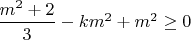
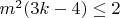
Что возможно только при
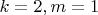
Допустим, что для фиксиранного

наименьшее решение

Аналогичное решение водит до аналогичный результат: