Решите уравнение

в натуральных числах.

А дальше как?
Вы сможете выделить время?
Задача вроде несложная, не увёрен в некоторых моментах, но путь

такой, вчера то, что смог за пару часов накидал в TexStudio, переношу сюда.
В продолжение того, что вы написали.
Поскольку

, любые два множителя

,

,

в
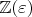
взаимно просты, кроме делителя

в случае

.

- простые элементы (

).
Разберём случай

.
Первый сомножитель

должен содержать оба сопряжённых простых (

и

), поэтому

Норма второго сомножителя обязана быть квадратом:

Положив

,

получаем

Если существует простое число

- делитель обоих множителей, то оно также должно делить их сумму и разность.
Из

, тогда

не может делить

, следовательно

.
Если

, то

, но

нечётно, так как

, что противоречит, что

.
Если

, то

, но

, что также противоречит. Следовательно

.
Так как

нечётно (из

), тогда

также нечётно, тогда

- нечётные, но их произведение

нечётно только если

нечётно, однако если

нечётно, то

, что невозможно для произведения двух нечётных, следовательно

- чётно,

- чётны.
Так, что можно положить

тогда

, при этом

Существует ровно два различных разложения произведения.
Кладём

в меньший множитель, тогда пусть

(здесь

), тогда

.
Получим:




Здесь

нечётно,

чётно, причём

,

.
Кладём

в меньший множитель, тогда пусть

(те же условия на

), тогда

.
Получим:




Здесь

чётно,

нечётно, причём

,

.
Разберём случай, когда

, тогда

где

,

.
Группа единиц

циклична:

, заменой

,

,

(с сохранением

) получаем:

При

ни один сомножитель не содержит простых

,

, поэтому каждый сомножитель является квадратом (с точностью до единиц).
Целочисленным можно сделать именно первый квадрат домножив при необходимости на единицу, тогда

.
Поскольку

и

, каждое такое

примитивно представимо формой

- это норма элемента

из

. Чтобы получить два независимых параметра, запишем

откуда

Так одна переменная

заменяется на пару

, при этом условие

гарантирует, что

.
Пусть

, из

получаем

Требование

даёт

Примитивное решение:

Тогда:



где

.