transcendentЯ всегда готов согласиться и признать ошибку, если есть конструктивные аргументы.
1. Пока, к сожалению, не могу согласиться с вашим утверждением, что мы вышли за пределы, где ВТФ должна работать, я рассматриваю решения в

, числа в

вложены в

. Отсутствие решений в

ведёт к отсутствию решений в

. Никто изначально не гарантивал, что нет решения ВТФ в кольце

для

. Если бы решение было, то можно было тем самым показать, что она разрешима в этом кольце, тогда это дало бы повод сомневаться, что в

ВТФ неразрешима. Но вывод говорит об обратном.
2. В

сумма квадратов неотрицательных чисел

может быть равна только если

и
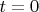
, это следует из неотрицательности норм квадратов элементов.
3. В доказательстве явно предполагается, что

.
Если бы существовало нетривиальное решение, его можно было бы масштабировать до взаимно простого, что противоречит условию.
Умножение на единицы не даст новых решений, т.к.

, но

обратим и условие

.
Система уравнений

и

действительно приводит к тривиальным решениям, это не насильственное сведение :), а результат линейной независимости

,

и отсутствие делителей нуля.
4. Комплексных чисел нет в

. Некорректно тут их использовать.