0 [[1, 27], [2, 2]]
1 [[1, 198], [2, 36], [3, 2]]
2 [[1, 374], [2, 228], [3, 89], [4, 30], [5, 7], [6, 2]]
3 [[1, 123], [2, 211], [3, 226], [4, 180], [5, 127], [6, 57], [7, 27], [8, 8], [9, 6], [10, 2]]
4 [[1, 9], [2, 26], [3, 60], [4, 117], [5, 165], [6, 179], [7, 162], [8, 120], [9, 77], [10, 41], [11, 30], [12, 10], [13, 3], [14, 1]]
5 [[1, 2], [2, 9], [3, 17], [4, 30], [5, 54], [6, 116], [7, 96], [8, 156], [9, 129], [10, 123], [11, 100], [12, 74], [13, 47], [14, 22], [15, 16], [16, 5], [17, 1], [18, 3]]
6 [[3, 8], [4, 20], [5, 37], [6, 80], [7, 115], [8, 133], [9, 152], [10, 121], [11, 115], [12, 86], [13, 59], [14, 38], [15, 21], [16, 6], [17, 5], [18, 2], [19, 2]]
7 [[2, 10], [3, 22], [4, 53], [5, 103], [6, 113], [7, 138], [8, 148], [9, 142], [10, 95], [11, 76], [12, 47], [13, 33], [14, 8], [15, 7], [16, 4], [18, 1]]
8 [[1, 19], [2, 53], [3, 102], [4, 158], [5, 166], [6, 169], [7, 131], [8, 92], [9, 51], [10, 33], [11, 16], [12, 4], [13, 1], [14, 1]]
9 [[1, 150], [2, 213], [3, 218], [4, 179], [5, 101], [6, 64], [7, 22], [8, 8], [9, 3]]
10 [[1, 332], [2, 235], [3, 117], [4, 37], [5, 17]]
11 [[1, 322], [2, 66], [3, 11], [4, 2]]
12 [[1, 108], [2, 12]]
13 [[1, 32]]
14 [[1, 3]]
15 [[1, 1]]
16 []
17 []
18 []

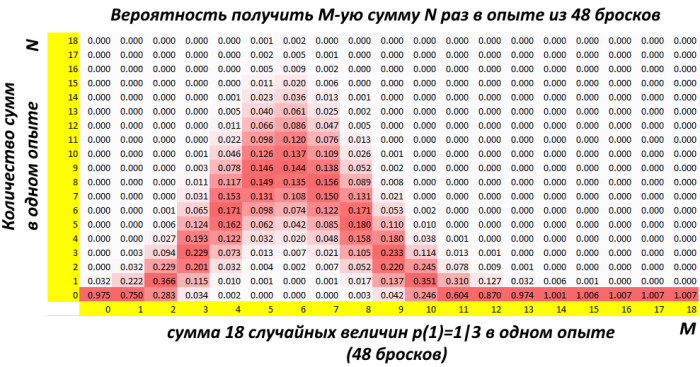
 крайне мала и равна около
крайне мала и равна около 
 до
до 
 , а вторая - с вероятностью
, а вторая - с вероятностью  , то сумма каждой половины подчиняется своему индивидуальному биномиальному распределению, а распределение суммы этих сумм (то, что мы имеем) - это некоторая свертка этих двух распределений. Это уже не биномиальное распределение.
, то сумма каждой половины подчиняется своему индивидуальному биномиальному распределению, а распределение суммы этих сумм (то, что мы имеем) - это некоторая свертка этих двух распределений. Это уже не биномиальное распределение. - нормальное распределение.
- нормальное распределение. , а десятые доли процента.
, а десятые доли процента. .
. . Отношение этих вероятностей
. Отношение этих вероятностей  , т.е. полученная комбинация в
, т.е. полученная комбинация в  раз менее вероятна, чем самая вероятная.
раз менее вероятна, чем самая вероятная.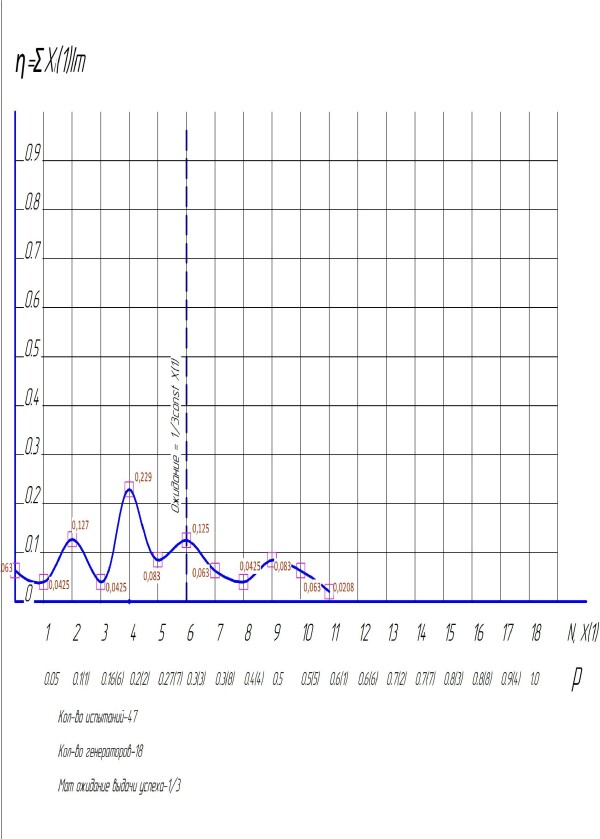
 , по аналогии для
, по аналогии для  , (если я правильно понял, что
, (если я правильно понял, что  ), для
), для  . Значит ли это, что для выпадения одновременного 18 " бинго" при ожидании "успеха" от одного генератора,
. Значит ли это, что для выпадения одновременного 18 " бинго" при ожидании "успеха" от одного генератора,  , вероятно понадобится порядка 387 миллионов сессий?, а для одновременного выпадения 18 "зерpо"- при
, вероятно понадобится порядка 387 миллионов сессий?, а для одновременного выпадения 18 "зерpо"- при  понадобится порядка 1580 сессий?
понадобится порядка 1580 сессий?