Искал ее еще в 2005 году, прослушивая курс теоретической физики, искал из философских соображений, самых (на мой взгляд) общих, и, кажется нашел вот сейчас- полная структура алгебры кватернионов:

Умножение элементов в таблице умножения группы

эквивалентно попарным композициям морфизмов(стрелок) в этой структуре.
Удивительно, что если достроить до шестиугольника, то в нем треугольники 2,3 повторяются дважды, а 1,4 встречаются один раз.
Надо попробовать замостить плоскость этой структурой и затем пронумеровать объекты(точки). По идее должны получить какое-то количество видов эквивалентных объектов (точек).
Прямолинейное перемещение по этой структуре на плоскости: FF,UU,TT,-U-U,-T-T,-F-F - это перемещения в эквивалентные точки. Поэтому

, а перемещения:

эквивалентно отсутствию перемещения. Перемещение

- тоже покой. Таким образом таблицу умножения группы

можно уточнить следующим образом:
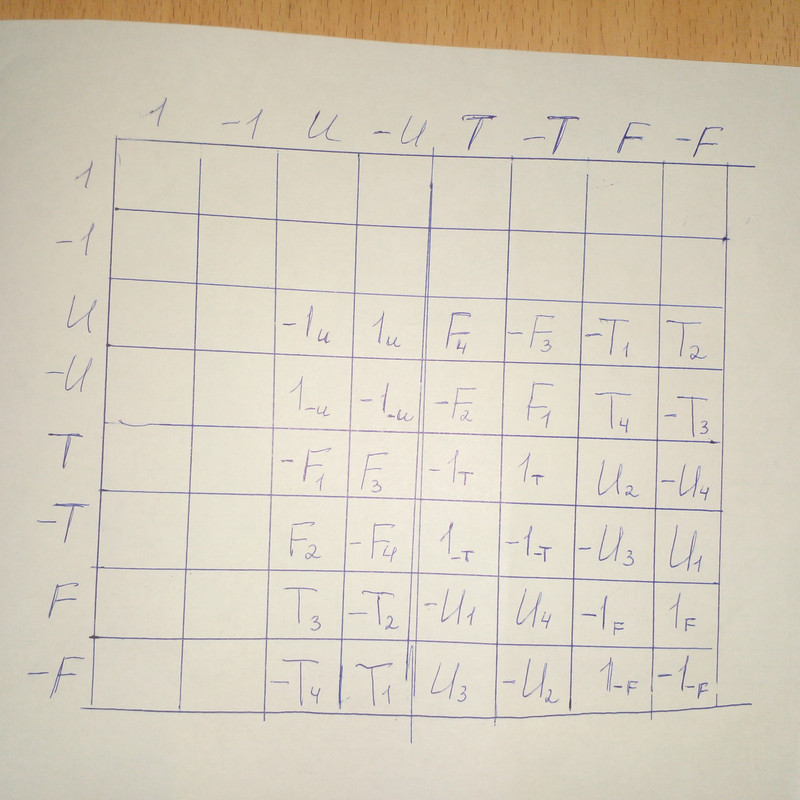
Из таблицы умножения видно, что всего возможно 4 треугольника и они пронумерованы на изображении алгебраической структуры. Индексы у букв, которыми мы обозначаем морфизмы(стрелки) в таблице умножения группы кватернионов обозначают: в результате композиции в каком из 4-х треугольников получен данный морфизм (стрелка, буква).
Посмотрел первую лекцию из предложенного цикла - не заходит. Не потому, что лекция плохая, наоборот, лекция очень хорошая, но не воспринимается сразу потому, что материал сложный и нет базовых знаний для него. Для того, чтобы он улегся в голове необходимо обсуждение, осмысление, время, освоение нотации, освоение всех применяемых понятий. Всё это очень сильно загромождает мозг, если осваивается не в обычном естественном и длительном общении, а в кратком курсе. Т.е. где-то неделю 2 на ежедневное обсуждение по теме этой лекции и можно переходить ко второй, а так- это в одно ухо влетело - в другое вылетело, может что-то где-то случайно зацепилось.
На первом рисунке на этой странице приведена диаграммная схема или предкатегория в терминологии ТК, это как раз структура алгебры кватернионов и кватернионной логики. Как увидеть здесь категорию и как ее оформить правильно? Какую нотацию для этого использовать? Мне для данного исследования было достаточно понятий стрелки и точки, далее все на интуиции. Но получается ситуация, когда есть понимание того, что ищется и что делается, а выразить это понимание на понятном языке не получается.
Логика алгебраических структур - это по сути движения по диаграммной схеме и правила регламентирующие эти движения.