их всего два
Да, два.
Первое определение. Матрица линейного преобразования

в базисе

- это такая матрица

, что

Второе определение. Матрица линейного преобразования

в базисе

- это такая матрица

, что

Наверное, Вы имели в виду

,

, иначе получается тождественное преобразование.
Если первый индекс у

мы будем интерпретировать как номер строки, то в первом определении координаты образов базисных векторов записываются в столбцы, а во втором определении -- в строки. Но можно про это вообще не думать. Определение имеет смысл без интерпретации матрицы в виде таблицы.
Да, конечно, определение имеет смысл без интерпретации матрицы в виде таблицы (если под матрицей понимать функцию

и тогда лучше сказать "без расположения элементов функции в виде таблицы"), но тогда это будет определение не преобразования, а только его функции

. Я сначала тоже думал как Вы, но потом написал:
Однако то, что я называл функцией преобразования то, что обычно называется матрицей преобразования, было неправильно:
одной функции

самой по себе недостаточно для определения линейного преобразования, нужно еще либо условие, что координата

перемножается с элементом
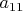
, координата

с элементом

и так далее, затем координата

перемножается с элементом

, координата

с элементом

и так далее, то есть номер координаты должен совпадать с первым индексом элемента функции

,
либо условие, что координата

перемножается с элементом
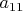
, координата

с элементом

и так далее, то есть номер координаты должен совпадать со вторым индексом элемента функции

.
(Я взял для второго условия другой вектор - вектор

.)
Одно из этих условий можно задать, если расположить элементы функции в виде двухмерной матрицы (причем это можно сделать двумя способами) и при этом положить, с какой стороны должно совершаться умножение матрицы на координаты преобразуемого вектора - справа или слева, - обычно полагается, что справа, и тогда выбирается второе условие.
Например, в учебнике Куроша "Курс высшей алгебры" принято второе определение. Но у него и значение оператора

на векторе

обозначается

и в координатах это выглядит как умножение вектора-строки на матрицу.
Да, и
nnosipov писал об этом:
Обозначение образа вектора при линейном преобразовании, где аргумент слева, а оператор справа, встречается в "Курсе высшей алгебры" Куроша.
в комментарии к моему
topic143328.html - я там предлагал обозначать преобразование не только как

, но и как

, в зависимости от ситуации. (Это сообщение изобилует оплошностями, которые я допустил по незнанию элементарных вещей.)
-- 16.11.2020, 11:18 --А вот с остальным ... Во всяком случае, если выбрать один из двух равноценных вариантов, то выбор будет носить случайный характер, а если указать оба, то случайного характера не будет, потому что будут указаны все возможные варианты - их всего два, но ... надо подумать.
Математики уже давно сделали выбор определения матрицы линейного оператора, и мир не рухнул. Так что все эти огороды напрасны.
Конечно, сделали выбор, и преобразуют векторы, но выбор этот был произвольный, и хотелось бы разобраться в том, какие были альтернативы. Зачем? Любые знания, кроме того, что сами по себе интересны, могут еще и помочь добыть другие знания.
-- 16.11.2020, 11:27 --Но мне кажется, можно предложить третье определение, которое не носит случайного характера -
линейное преобразование определяется функцией

, которая сопоставляет на множестве

каждой паре

некоторое число

вместе с одним из условий
Что ж Вас не отпустит никак?
Определив функцию двух натуральных переменных, Вы уже определили матрицу.
Нет, можете почитать об этом в моем комментарии на несколько абзацев выше.