В чём смысл этого? Очевидно, что

(для целых

и

, для нецелых тривиально обобщается).
-- 05 дек 2020, 17:55 --На самом деле, это скорее относится к первому сообщению. В вашем втором больше смысла, признаю.
-- 05 дек 2020, 17:58 --Ну вот вы ведь сами понимаете, что ваши "интегралы"
![$\int\limits_0^\infty \sin{[x^2]}\,dx$ $\int\limits_0^\infty \sin{[x^2]}\,dx$](https://dxdy-02.korotkov.co.uk/f/5/0/4/5048453b4b0079082e995938aa915dab82.png)
,
![$\int\limits_0^\infty e^{-[x^2]}\,dx$ $\int\limits_0^\infty e^{-[x^2]}\,dx$](https://dxdy-02.korotkov.co.uk/f/9/0/f/90fbe8a355a193199f5a1ae362ed4c1782.png)
- никоим образом не интегралы?
-- 05 дек 2020, 18:06 --Если что, то первый суммо-интеграл даже не сходится, а второй сходится к

(я не сумел набрать знак тета-функции, это наиболее похожий на него).
-- 05 дек 2020, 18:17 --Хотя нет, это у меня бред,
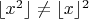
.
-- 05 дек 2020, 18:22 --Хорошо, в этом случае формула меняется:

.
-- 05 дек 2020, 18:33 --Первый суммо-интеграл сходится (если вообще сходится) очень медленно (UPD: такой же метод, как для второго суммо-интеграла (в данном случае - сведением синуса к мнимой части комплексной экспоненты) не работает, так как тот ряд гарантированно сходится лишь при

(

- коэффициент вместо

в степени экспоненты)), второй сходится к
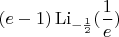
.