Вот
Я тут немного расписал:
Пусть есть независимые случайные величины
![$X_1, ..., X_n \sim U[0, 1]$ $X_1, ..., X_n \sim U[0, 1]$](https://dxdy-03.korotkov.co.uk/f/a/0/6/a06a76efbf6ca585db90fcc6dc5a081682.png)
. Нужно найти
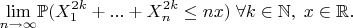
Для начала применим ЗБЧ Хинчина:

Из этого заключаем, что все такие суммы, представленные в числителе сходятся к одному матожиданию, для определённости рассмотрим матожидание первой величины и найдём его:

Тогда искомая вероятность будет стремиться к функции распределения вырожденного закона в точке

.
Для

Осталось найти предел только в этой точке.
Далее можно найти дисперсию для сведения к виду ЦПТ Хинчина, но это не обязательно.
Сводим к ЦПТ:
 Ответ
Ответ: два предела -

и

.
-- 08.05.2020, 15:22 --Дисперсию найти.
Необязательно ведь.
Это верно, но
Конечно, это условие есть, забыл написать.
есть независимость
Есть.
бесплатно на

поделить
Так уже - я бы не получил просто ЗБЧ, а я применил его, чтобы показать, что у всех с.в. одно матожидание.
украду-ка я эту задачку
На здоровье)
криво
Хорошо:
![$p_X(x) = \dfrac{1}{b - a} \overset{b = 1, a = 0}{=} 1 \; \forall x \in [0, 1]; 0 \;- otherwise.$ $p_X(x) = \dfrac{1}{b - a} \overset{b = 1, a = 0}{=} 1 \; \forall x \in [0, 1]; 0 \;- otherwise.$](https://dxdy-03.korotkov.co.uk/f/e/e/2/ee29ee81786fa6895d74f84f50349d1c82.png)
Показательного, хи-квадрат, Релея
Интересно, таких распределений у нас в программе не было, почитаю.