Да.
Ага. Да и вообще, там ошибка у меня была, в выкладках.
Оно не имеет отношения к задаче.
Ну, какое-то отношение имеет, хотя эт и не решение...
за интеграл
Ну вот пусть он есть

и равен

, так что

и

. На этой поверхности получается вполне себе приличный дифур (хотя и не решабельный в элементарных). Так что решения с какими-то нач. условиями (в том числе, и со странным ограничением, непонятно откуда взявшимся, из первого поста) есть.
Понятно, что исходный функционал не ограничен ни сверху, ни снизу: мы можем уехать за границу - в область отрицательных а-бэ, зашибить там бешеные (отрицательные) бабки, и за небольшую плату вернуться в нужное место. Тем не мене, вопрос о его критических точках - решениях ур-я Эйлера-Лагранжа - вполне себе законен, они - есть, непонятно какие, правда. Ну и ладно.
Единственно, что боле-мене решабельно - это отыскание частных решений с

(что, собственно, уже и делалось). Это приводит к дифуру

, решая который, находим
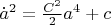
, и из условия

получим окончательно

(т.е., случай

- не подходит.
Он, фактически, будет предельным для построенных решений, но решением - не, не будет). Ну, и решение теперь выражается через эллиптические интегралы. Что, конечно, не фонтан.
Впрочем, что-то уже и можно сказать. Типа: если
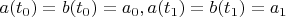
, то: по этим данным ищем такое

, что

. Уже отсюда видно: иногда решение единственно; иногда их - два (?), но иногда - когда разность

уж очень велика - их нет. Вроде - так.