Вы указали требование (назовем его условие А)

Его избыточность заключается вот в чем. Условие А вовсе не является необходимым для существования решения. Вы этого и не утверждали,
я просто это отметил. Контр-пример - матрица у которой все элементы равны нулю, кроме
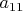
. Решением будет

.
Насчет того, что достаточно одного определителя, формулирую в виде теоремы.
Теорема. Пусть выполнено условие А и определитель матрицы
составленной из 1-го, 2-го столбцов и правой части равен нулю. Тогда указанная система имеет решение.
Док-во: Из условия А следует, что 1-й и 2-й столбцы линейно независимы. Если определитель матрицы составленной из 1-го, 2-го столбцов и правой части
равен нулю, то эти векторы линейно зависимы и

линейная комбинация равная нулю.
В ней коэф. при св. члене (ну и тогда естественно еще какой-то) не равен нулю. Получаем решение.