Они не равны нулю, и если я нашел, что они нулевые,
то, тем самым, пришел к противоречию.
Да где вы это нашли-то?
Можно например принять такое индуктивное определение семейства функционалов

на последовательностях элементов коммутативных групп (скорее всего коммутативность и не нужна, но тогда придется внимательно следить):

,

.
Эквивалентное определение -

при

определяется как обычно, а при

положим

.
Кажется вы тут считаете что

. Но это совершенно не обязано быть правдой - в приведенном
svv правиле (которое мне кажется единственным разумным вариантом обобщения функционала
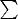
на случай, когда верхний индекс меньше нижнего), нужно, чтобы вторая сумма начиналась с индекса, следующего за тем, на которым закончилась предыдущая.
Что ИМХО неудобно - гораздо лучше считать, что верхний индекс не включается. Получаемый функционал

удовлетворяет свойствам

,

. Соответственно если

, то

(берется обычное определение суммы). И есть та же симметрия, что в интеграле

. Фактически получается что

- это интеграл Римана-Стилтьеса по ступенчатой функции от какой-то функции, которая в окрестности точки

равна

.