Вот что придумал. Берем раздувающуюся окружность, то есть такую окружность, радиус которой растет. На окружности две точки, одна неподвижна, вторая движется, удаляясь от первой, причем удаляется не только просто из-за увеличения длины окружности (радиус ведь растет), а еще и в результате своего движения по окружности. Пусть расстояние

вдоль окружности между точками является функцией радиуса, то есть

. Значит, можно записать и наоборот

. Стандартным образом находим производную

. Выражаем

через полярный угол

, подставляем в обе формулы, и перед нами какая-о спираль

в полярных координатах и ее производная
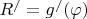
, также в полярных координатах. Понятно, что изменяя зависимость

от

можно получить на выходе любую спираль. Значит, любая спираль, записанная в полярных координатах, имеет производную, записанную в полярных координатах. Я прав?