Производная по вектору

[Munin]

Ruben в сообщении #1401056 писал(а):

Блин..извините. Когда увидел того крокодила, то решил, что это не про меня) А вы когда процитировали, то вроде и не крокодил уже ))

Да, на крокодила формула очень похожа, отличное сравнение! :-)

Ruben в сообщении #1401056 писал(а):

Скажем, нам надо найти градиент такой функции:

$$f(\mathbf{r}) = \left\lVert \mathsf{A}\cdot \mathbf{r} \right\rVert ^2$$

Дело в том, что квадрат - это не матричная операция. Чтобы найти матричную, надо сделать в лучшем случае $\|\mathsf{A}\cdot\mathbf{r}\|^2=(\mathsf{A}\cdot\mathbf{r})^\mathrm{T}(\mathsf{A}\cdot\mathbf{r}).$ И потом уже искать производную. Что-то в духе $(\mathsf{A}\cdot\mathbf{r})^\mathrm{T}\mathsf{A}$ и получится.

Утундрий в сообщении #1401066 писал(а):

Так сходу и не упомню, где еще видал эту "производную по вектору", кроме как у Ландау&Лифшица.

Ой, да она много где, только обычно под разными названиями и обозначениями. В Тамме она $(\mathbf{v}\nabla)$ или $(\mathbf{v}\operatorname{grad}).$ В тензорах $v^i\dfrac{\partial}{\partial x^i},$ правда, обычно не рассматривается как отдельная операция. В дифференциальной геометрии - уже скорее $\nabla_\mathbf{v}$ или $\mathcal{L}_\mathbf{v}.$ Думаю, если перебрать все варианты обозначений, много где видели.

[Ruben]

Mikhail_K в сообщении #1401060 писал(а):

Ruben
Используйте такое определение градиента: $f(r+h)-f(r)=f^\prime(r)h+o(\|h\|)$.
(Здесь я вместо $\frac{\partial f(r)}{\partial r}$ пишу более привычное для меня обозначение $f^\prime(r)$; векторы $r$ и $h$ одной размерности.)
Точнее это определение надо понимать так: если мы при любом $h$ и конкретном $r$ представили левую часть $f(r+h)-f(r)$ в виде $ah+o(\|h\|)$, где $a$ - некоторая вектор-строка, то она и есть $f^\prime(r)$.

Когда начал читать, то мысленно уже отмахнулся от вашего комментария, т.к. первым постом я написал почти это же, с тем отличием, что я сразу выписал линейную часть приращения. Но тут понял, что определение как раз и содержит метод вычисления производной. А тут и комментарии Munin-а как раз пришлись к месту:

Munin в сообщении #1401082 писал(а):

Дело в том, что квадрат - это не матричная операция. Чтобы найти матричную, надо сделать в лучшем случае $\|\mathsf{A}\cdot\mathbf{r}\|^2=(\mathsf{A}\cdot\mathbf{r})^\mathrm{T}(\mathsf{A}\cdot\mathbf{r}).$ И потом уже искать производную.

Поехали:

$$f(\mathbf{r}) = (\mathsf{A}\cdot\mathbf{r})^\mathrm{T}(\mathsf{A}\cdot\mathbf{r})$$

$$f(\mathbf{r}+\mathbf{h}) - f(\mathbf{r}) = (\mathsf{A}\cdot(\mathbf{r}+\mathbf{h}))^\mathrm{T}(\mathsf{A}\cdot(\mathbf{r}+\mathbf{h})) - (\mathsf{A}\cdot\mathbf{r})^\mathrm{T}(\mathsf{A}\cdot\mathbf{r}) = (\mathsf{A}\cdot\mathbf{h})^\mathrm{T} \cdot (\mathsf{A}\cdot\mathbf{r}) + (\mathsf{A}\cdot\mathbf{r})^\mathrm{T} \cdot (\mathsf{A}\cdot\mathbf{h}) + o(\mathbf{h})$$

$$\mathrm{df} = \left((\mathsf{A}\cdot\mathbf{r})^\mathrm{T} \cdot (\mathsf{A}\cdot\mathbf{h})\right)^\mathrm{T} + (\mathsf{A}\cdot\mathbf{r})^\mathrm{T} \cdot (\mathsf{A}\cdot\mathbf{h}) = 2(\mathsf{A}\cdot\mathbf{r})^\mathrm{T} \cdot \mathsf{A}\cdot\mathbf{h}$$

$$\nabla{\mathrm{f}} = 2(\mathsf{A}\cdot\mathbf{r})^\mathrm{T} \cdot \mathsf{A}$$

Спасибо! это было полезно и эффективно.

Mikhail_K в сообщении #1401060 писал(а):

Искать "формальный способ получать правильные ответы" я бы не советовал.

Отнюдь, считаю, что это вполне хорошее занятие. В конце-концов, в попытках найти "формальный способ получения правильных ответов" и возникают разные методы. Так вот, возвращаясь к методам, хотелось бы к моему примеру как-то применить формулу производной, упоминаемую Munin-ом:

Цитата:

$$\dfrac{\partial(y_1, \ldots, y_k)}{\partial(x_1, \ldots, x_n)}=\dfrac{\partial(y_1, \ldots, y_k)}{\partial(u_1, \ldots, u_m)}\dfrac{\partial(u_1, \ldots, u_m)}{\partial(x_1, \ldots, x_n)}$$

То есть, либо понять, как это делается, или понять, почему этого сделать нельзя. Потому что как уже правильно заметили Someone и Munin, так вульгарно, как я её применил к скалярному произведению, делать нельзя.

[Munin]

Ruben в сообщении #1401056 писал(а):

Скажем, нам надо найти градиент такой функции:

$$f(\mathbf{r}) = \left\lVert \mathsf{A}\cdot \mathbf{r} \right\rVert ^2$$

Пользуясь правилом цепочки, я получаю:

$$\cfrac{ \partial f (\mathbf{r})}{\partial \mathbf{r}} = 2\left (\mathsf{A}\cdot \mathbf{r} \right ) \mathsf{A} $$

Видимо, что-то в консерватории не так.

Цитата:

$$\dfrac{\partial(y_1, \ldots, y_k)}{\partial(x_1, \ldots, x_n)}=\dfrac{\partial(y_1, \ldots, y_k)}{\partial(u_1, \ldots, u_m)}\dfrac{\partial(u_1, \ldots, u_m)}{\partial(x_1, \ldots, x_n)}$$

Распишем в три функции (а не две):

$\begin{aligned} g(x)&=x^2 \\ h(\mathbf{r})&=\|\mathbf{r}\| \\ \mathbf{k}(\mathbf{r})&=\mathsf{A}\cdot\mathbf{r} \\ f(\mathbf{r})&=g(h(\mathbf{k}(\mathbf{r})))\end{aligned}$

Тогда:

$\begin{aligned} g\colon&\mathbb{R}\to\mathbb{R} \\ h\colon&\mathbb{R}^n\to\mathbb{R} \\ \mathbf{k}\colon&\mathbb{R}^n\to\mathbb{R}^n\end{aligned}$

Матрицы Якоби будут, соответственно, размеров $1\times 1,1\times n,n\times n$:

$\begin{aligned} \dfrac{\partial g}{\partial x}&=2x \\ \dfrac{\partial h}{\partial(x_1,\ldots,x_n)}&=\dfrac{(x_1,\ldots,x_n)}{\sqrt{x_1^2+\ldots+x_n^2}} \\ \dfrac{\partial(k_1,\ldots,k_n)}{\partial(x_1,\ldots,x_n)}&=\mathsf{A},\qquad\text{т. е., }\dfrac{\partial k_i}{\partial x_j}=\mathsf{A}_{ij}.\end{aligned}$

Всех их вместе соберём:

$$\dfrac{\partial f(\mathbf{r})}{\partial\mathbf{r}}=2h(\mathbf{k}(\mathbf{r}))\cdot\dfrac{(\mathbf{k}(\mathbf{r}))^\mathrm{T}}{\|\mathbf{k}(\mathbf{r})\|}\cdot\mathsf{A}=2\|\mathsf{A}\cdot\mathbf{r}\|\cdot\dfrac{(\mathsf{A}\cdot\mathbf{r})^\mathrm{T}}{\|\mathsf{A}\cdot\mathbf{r}\|}\cdot\mathsf{A}=2(\mathsf{A}\cdot\mathbf{r})^\mathrm{T}\cdot\mathsf{A}.$$

Что и требовалось доказать.

[Ruben]

Munin в сообщении #1401554 писал(а):

Видимо, что-то в консерватории не так.

В моём случае скорее в училище ))

Цитата:

Что и требовалось доказать.

Здорово! Но выходит, я до того, как написать сюда, делал почти это же, с той разницей, что

$$\dfrac{\partial h(\mathbf{k})}{\partial\mathbf{k}}=\dfrac{\mathbf{k}}{\|\mathbf{k}\|}$$

То есть, производную по модулю я взял без транспонирования, а точно в таком же виде, как если бы брал производную от скаляра. Откуда и результат. Я так понял, что всегда когда мы берём "производную по вектору", т.е. вычисляем градиент на неком векторном пространстве, то всегда должны следить, чтобы результат был строкой.

Да, кстати. Ваше замечание

Munin в сообщении #1401082 писал(а):

Дело в том, что квадрат - это не матричная операция. Чтобы найти матричную, надо сделать в лучшем случае $\|\mathsf{A}\cdot\mathbf{r}\|^2=(\mathsf{A}\cdot\mathbf{r})^\mathrm{T}(\mathsf{A}\cdot\mathbf{r}).$ И потом уже искать производную.

получается, относилось не к этому способу, а к способу поиска производной через определение, как мне подсказал Mikhail_K ? Потому что вы использовали и модуль и квадрат.

[ewert]

Хм. Ну дифференциал квадратичной формы есть, очевидно,

$d((G\vec x,\vec x), \vec h)=d({\vec x}^{\mathrm T}\cdot G\cdot\vec x, \vec h)={\vec h}^{\mathrm T}\cdot G\cdot\vec x+{\vec x}^{\mathrm T}\cdot G\cdot\vec h.$

Второе слагаемое выглядит нормально, а вот первое -- нет, т.к. приращение $\vec h$ стоит под знаком транспонирования и умножается не с той стороны. Однако ${\vec a}^{\mathrm T}\cdot\vec b$ -- это то же самое, что и ${\vec b}^{\mathrm T}\cdot\vec a$, поэтому

$d((G\vec x,\vec x), \vec h)={(G\cdot\vec x)}^{\mathrm T}\cdot\vec h+{\vec x}^{\mathrm T}\cdot G\cdot\vec h={\vec x}^{\mathrm T}\cdot G^{\mathrm T}\cdot\vec h+{\vec x}^{\mathrm T}\cdot G\cdot\vec h,$

т.е. $(G\vec x,\vec x)'={\vec x}^{\mathrm T}\cdot(G^{\mathrm T}+G)$. Это вообще говоря. Но в нашем случае матрица $G=A^{\mathrm T}A$ симметрична, поэтому и

${(\|A\vec x\|^2)}'={(A^{\mathrm T}A\vec x,\vec x)}'=2{\vec x}^{\mathrm T}A^{\mathrm T}A.$

[Munin]

(Оффтоп)

Ruben в сообщении #1401744 писал(а):

В моём случае скорее в училище ))

Это же цитата из Жванецкого.

-- 27.06.2019 15:31:36 --

Ruben в сообщении #1401744 писал(а):

Я так понял, что всегда когда мы берём "производную по вектору", т.е. вычисляем градиент на неком векторном пространстве, то всегда должны следить, чтобы результат был строкой.

В общем, да.

[Ruben]

Всем спасибо за ответы, мне понравилось и было для меня полезно! Во процессе обдумывания ваших ответов, возник вопрос, над которым я раньше как-то не задумывался: скалярное произведение - это всё-таки $\mathbf{a} \cdot \mathbf{b}$ или $\mathbf{a}^\mathrm{T} \cdot \mathbf{b}$ ? Если у нас есть базис, то раскладывая по нему, подходит первый вариант. А второй вариант вообще какой-то универсальный. Разъясните, пожалуйста.

-- 30.06.2019, 09:30 --

(Оффтоп)

Munin в сообщении #1401815 писал(а):

Ruben в сообщении #1401744 писал(а):

В моём случае скорее в училище ))

Это же цитата из Жванецкого.

Знаю)) Я же сразу погуглил источник вашей аллюзии))

[Mikhail_K]

Ruben в сообщении #1402292 писал(а):

скалярное произведение - это всё-таки $\mathbf{a} \cdot \mathbf{b}$ или $\mathbf{a}^\mathrm{T} \cdot \mathbf{b}$ ?

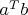
Здесь есть такая тонкость. Запись $a^Tb$ имеет смысл, если $a$ и $b$ - вектор-столбцы, то есть матрицы $n\times 1$. Скалярное произведение (я привык обозначать его $(a,b)$, хотя запись $a\cdot b$ тоже встречается, особенно в физике) имеет смысл, если $a$ и $b$ - элементы любого евклидова пространства (любой природы).

Это именно тонкость, потому что, во-первых, вектор-столбцы заданного размера образуют евклидово пространство, а с другой стороны, в любом евклидовом пространстве конечной размерности можно зафиксировать ортонормированный базис и взаимно-однозначно представить любые его элементы вектор-столбцами. Во многих случаях, можно и не различать вектор-столбцы и элементы произвольного конечномерного евклидова пространства (говорят, что все евклидовы пространства одной и той же конечной размерности изоморфны, в частности изоморфны соответствующему пространству вектор-столбцов; изоморфны - значит, грубо говоря, имеют одинаковые свойства и их можно отождествить между собой). 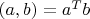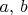Эта тонкость, это различие начинает "вылезать", во-первых, если мы хотим рассматривать несколько базисов в одном пространстве и переходить между ними; во-вторых, если нас интересуют бесконечномерные пространства; в-третьих, если мы в пространстве с заданным фиксированным базисом вводим "нестандартное" скалярное произведение, то есть не по формуле $(a,b)=a^Tb$ (где буквами $a,\,b$ я для простоты обозначил как элементы пространства, так и соответствующие вектор-столбцы), а по формуле $(a,b)=a^TAb$, где $A$ - симметричная (в комплексном случае - эрмитова) положительно определённая матрица. (Впрочем, для такого скалярного произведения всё равно найдётся базис, в котором оно будет выглядеть как "стандартное".)

А по большому счёту, если про существование таких тонкостей помнить - то неважно, как что обозначать. Тот же градиент функции, с которого началась эта тема. В каких-то учебниках его считают вектор-строкой, в каких-то - вектор-столбцом. Это неважно, потому что всё равно каждой вектор-строке взаимно-однозначно соответствует вектор-столбец; также можно говорить просто про векторы как упорядоченные наборы из $n$ чисел, не уточняя, строки это или столбцы (тогда, конечно, нельзя будет говорить про "транспонирование" и подобные штуки, но к большим неудобствам это не приведёт).

[ewert]

Mikhail_K в сообщении #1402294 писал(а):

Тот же градиент функции, с которого началась эта тема. В каких-то учебниках его считают вектор-строкой, в каких-то - вектор-столбцом. Это неважно

Это достаточно важно, поскольку тут есть реальная методическая проблема. Я, например, вынужден одновременно рассматривать его и как строку и как столбец. Как частный случай матрицы Якоби это, естественно, строка (при стандартной интерпретации самих векторов как столбцов). Но когда дело доходит до производных по направлению и вообще до векторного анализа -- приходится переобуваться на бегу и называть его столбцом.

Выбирать что-то одно -- крайне неудобно. К счастью, эта эклектика вполне безобидна, пока рассматриваются только ортогональные преобразования координат. Но приходится специально переход к другой интерпретации оговаривать и оправдываться за него.

[arseniiv]

Мне казалось, тут всё просто. Дифференциал — строка, градиент — столбец, полученный поднятием индекса у дифференциала.

[ewert]

arseniiv в сообщении #1402319 писал(а):

Дифференциал — строка, градиент — столбец, полученный поднятием индекса у дифференциала.

Это только после того, как дойдёшь до тензорного анализа. А я про обычный матан.

(кстати, дифференциал -- это не строка)

[arseniiv]

Я подумал, мы на волне евклидовости здесь немножко отождествляем ковекторы со строками и векторы со столбцами.

ewert в сообщении #1402322 писал(а):

Это только после того, как дойдёшь до тензорного анализа. А я про обычный матан.

Методически не знаю, но со стороны кажется, что воспринимать градиент то как вектор, то как ковектор неудобнее, чем называть одно так, а другое эдак.

[ewert]

arseniiv в сообщении #1402324 писал(а):

со стороны кажется, что воспринимать градиент то как вектор, то как ковектор неудобнее, чем называть одно так, а другое эдак.

Это со стороны. А если нет разделения на векторы и ковекторы (нет ни времени, ни необходимости)?

[arseniiv]

Тогда и строки со столбцами не надо различать. По-моему, и логично, и практично.

[Ruben]

А давайте попробуем на примере. Допустим, у нас есть соглашение, что $\dfrac{\partial f(\mathbf{r})}{\partial\mathbf{r}}$ - столбец. Если последовательно брать производные как продемонстрировано в этом посте Munin-а, то столбец окажется слева от матрицы (в данном случае транспонированной). Можно (и нужно), конечно, их поменять местами, но это уже будет как-то неестественно...То есть, выглядит это так, как если мы перемножили последовательно матрицы Якоби, потом увидели, что матрица на столбец не умножается, и пока никто не видит поменяли их друг с другом местами ))