Решение на каком уровне предполагается?
Могу предложить следующий путь.
1) Показываем, что для каждого

и каждого

существует такое

, что для всех

, кроме, может быть, точки

, выполняется неравенство

, так что на всём указанном интервале существует не более одной точки, в которой

.
2) Берём

, где

. Множество всех интервалов вида

является покрытием

; так как

имеет счётную базу (например, множество интервалов с рациональными концами), из этого покрытия можно выбрать счётное подпокрытие, откуда следует, что множество

не более, чем счётно.
3) Множество

не более чем счётно и содержит все точки

, в которых
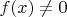
. Во всех же остальных точках функция равна

.