Mathew Rogan, спасибо, книгу сейчас попробую разыскать.
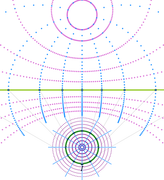
По поводу пространственной инверсии всё ещё есть сомнения. Если взять известную ситуацию с равномерно заряженной сферой, и отобразить "по инструкции" точки исходного пространства (с которыми должны, по идее, совпадать линии равного потенциала и "силовые линии"), картина отображения получается неожиданная (рисунок в прищепке).
Исходная сфера внизу (тёмно-зелёная окружность и сетка координат). Вверху, вокруг зелёной линии - инверсия её координатной сетки.
Построение автоматическое, точка-в-точку по формуле из учебника.
Равномерно заряженная сфера отобразилась в бесконечную плоскость (зелёная прямая), но словно в незаряженную, а весь заряд остался в центре инверсии. Картина очень похожа на поле "заряда над плоскостью". Часть, которая выше зелёной линии - это отображение внутренности сферы. Там всё сходится к центру шара. Электрического поля, конечно, нет, это лишь координатная сетка.
Испробую ещё одну гипотезу. Вместо расчёта плотности заряда по известному потенциалу - оставить весь заряд в центре инверсии (с обратным знаком), а само тело считать незаряженным, проинвертировать и посчитать поле в такой системе.
 -- 17.01.2019, 21:59 --
-- 17.01.2019, 21:59 --Формула и вправду работает. Остаётся разобраться с самим методом.
Такие результаты вызывают чувство досады. Наверное, не только у меня бывает - когда после долгих безуспешных попыток решить задачу выясняется, что решение-то было вполне простое.
