Решаю задачи по физике из сборника Чешева. Должен сказать, уровень задач этого сборника очень высок - в техническом плане эти задачи сложнее чем задачи Всеросса. Я взялся за одну из данных задач - получилось так, что ответ почти совпал, идея решения также в целом совпала, но я, похоже, совершил либо математическую ошибку, либо, что еще хуже, идейную. Прошу формучан проверить уровень строгости моего решения и, быть может, дать некоторые советы.
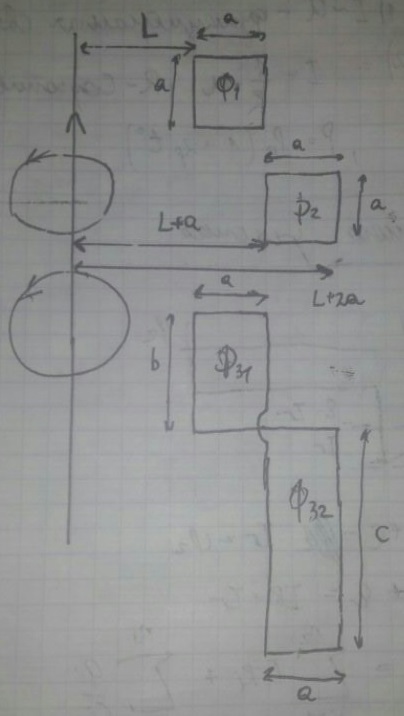
Задача: По бесконечно длинному проводнику течет переменный ток (на рисунке он течет снизу вверх). В плоскости провода расположены три проволочных контура, изготовленные из одного куска провода. Контуры 1 и 2 - квадраты, а третий контур состоит из двух прямоугольников со сторонами

и

. В некоторый момент времени через контуры 1 и 2 текут соответственно токи

. Найти ток

в контуре 3 в данный момент времени.
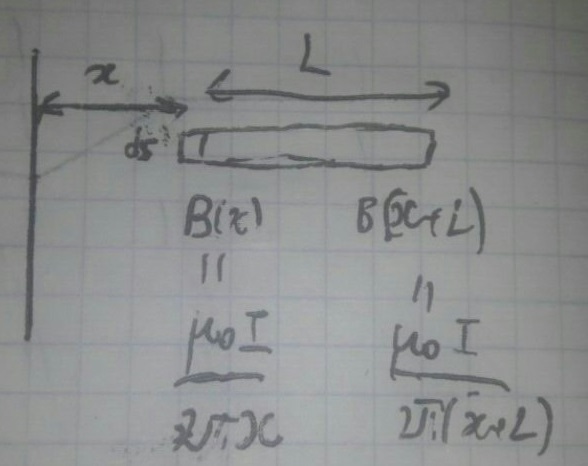
Для начала я решаю вспомогательную задачу: Пусть прямоугольный контур площадью

находится на расстоянии

от провода, ширина прямоугольника равна

(дабы строго не определять эти величины отмечу, что для контуров 1 и 2 расстояния до них от провода соответственно равны

и

, а их ширина равна

). Тогда поток

через контур равен
![$$\[\Phi = \ln \left( {1 + \frac{L}{x}} \right)\frac{{{\mu _0}IS}}{{2\pi }}\]$$ $$\[\Phi = \ln \left( {1 + \frac{L}{x}} \right)\frac{{{\mu _0}IS}}{{2\pi }}\]$$](https://dxdy-03.korotkov.co.uk/f/2/b/f/2bfe2cfa71db6f7918037012a003484382.png)
Для доказательства этого утверждения рассмотрим тонкую полоску площадью

- горизонтальный разрез контура. Магнитное поле в точках полоски меняется от значения
![$\[B(x) = \frac{{{\mu _0}I}}{{2\pi x}}\]$ $\[B(x) = \frac{{{\mu _0}I}}{{2\pi x}}\]$](https://dxdy-02.korotkov.co.uk/f/5/3/a/53a15e1cd9bc079c6b1aa1a10e686df382.png)
,
![$\[B(x + L) = \frac{{{\mu _0}I}}{{2\pi \left( {x + L} \right)}}\]$ $\[B(x + L) = \frac{{{\mu _0}I}}{{2\pi \left( {x + L} \right)}}\]$](https://dxdy-01.korotkov.co.uk/f/8/a/9/8a931eeafdc3fedfa0be45be2a4e0c6a82.png)
. Для элемента контура поток

равен
![$$\[d\Phi = \frac{{{\mu _0}I}}{{2\pi x}}dxds\]$$ $$\[d\Phi = \frac{{{\mu _0}I}}{{2\pi x}}dxds\]$$](https://dxdy-03.korotkov.co.uk/f/a/2/3/a23c45210c748137c904e1454c43646f82.png)
Насколько я представляю, математики далее пишут (в моем извращенном некомпетентном понимании) так:
![$$\[\Phi = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S
{\frac{{{\mu _0}I}}{{2\pi x}}dxds} = \ln \left( {x + L} \right)\frac{{{\mu _0}IS}}{{2\pi }} - \ln \left( x \right)\frac{{{\mu _0}IS}}{{2\pi }} = \ln \left( {1 + \frac{L}{x}} \right)\frac{{{\mu _0}IS}}{{2\pi }}\]$$ $$\[\Phi = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S
{\frac{{{\mu _0}I}}{{2\pi x}}dxds} = \ln \left( {x + L} \right)\frac{{{\mu _0}IS}}{{2\pi }} - \ln \left( x \right)\frac{{{\mu _0}IS}}{{2\pi }} = \ln \left( {1 + \frac{L}{x}} \right)\frac{{{\mu _0}IS}}{{2\pi }}\]$$](https://dxdy-01.korotkov.co.uk/f/8/3/d/83dfd4d34ebaf1a57404b6b50ab7066582.png)
Применим эту формулу для нахождения потоков
![$\[{\Phi _1},{\Phi _2},{\Phi _{31}},{\Phi _{32}}\]$ $\[{\Phi _1},{\Phi _2},{\Phi _{31}},{\Phi _{32}}\]$](https://dxdy-04.korotkov.co.uk/f/7/5/8/758cd5c4c30200b73ae221857d72b49682.png)
:
![$$\[\begin{array}{l}
{\Phi _1} = \ln \left( {1 + \frac{a}{L}} \right)\frac{{{\mu _0}I{a^2}}}{{2\pi }},{\Phi _2} = \ln \left( {1 + \frac{a}{{L + a}}} \right)\frac{{{\mu _0}I{a^2}}}{{2\pi }},{\Phi _{31}} = \ln \left( {1 + \frac{a}{L}} \right)\frac{{{\mu _0}Iab}}{{2\pi }},\\
{\Phi _{32}} = \ln \left( {1 + \frac{a}{{L + a}}} \right)\frac{{{\mu _0}Iac}}{{2\pi }}
\end{array}\]$$ $$\[\begin{array}{l}
{\Phi _1} = \ln \left( {1 + \frac{a}{L}} \right)\frac{{{\mu _0}I{a^2}}}{{2\pi }},{\Phi _2} = \ln \left( {1 + \frac{a}{{L + a}}} \right)\frac{{{\mu _0}I{a^2}}}{{2\pi }},{\Phi _{31}} = \ln \left( {1 + \frac{a}{L}} \right)\frac{{{\mu _0}Iab}}{{2\pi }},\\
{\Phi _{32}} = \ln \left( {1 + \frac{a}{{L + a}}} \right)\frac{{{\mu _0}Iac}}{{2\pi }}
\end{array}\]$$](https://dxdy-03.korotkov.co.uk/f/6/7/5/6752d516e2ab57bca6e9336fa91779ff82.png)
![$$\[{\Phi _3} = {\Phi _{31}} + {\Phi _{32}} = \frac{{{\mu _0}I}}{{2\pi }}\left( {ac\ln \left( {1 + \frac{a}{{L + a}}} \right) + ab\ln \left( {1 + \frac{a}{L}} \right)} \right)\]$$ $$\[{\Phi _3} = {\Phi _{31}} + {\Phi _{32}} = \frac{{{\mu _0}I}}{{2\pi }}\left( {ac\ln \left( {1 + \frac{a}{{L + a}}} \right) + ab\ln \left( {1 + \frac{a}{L}} \right)} \right)\]$$](https://dxdy-01.korotkov.co.uk/f/4/5/c/45cabc685d040ef57ffada62d6a0c7a382.png)
По закону электромагнитной индукции:
![$$\[\begin{array}{l}
\left| {{{\cal E}_1}} \right| = \frac{{d{\Phi _1}}}{{dt}} \sim \ln \left( {1 + \frac{a}{L}} \right)\frac{{{\mu _0}{a^2}}}{{2\pi }},\left| {{{\cal E}_2}} \right| = \frac{{d{\Phi _2}}}{{dt}} \sim \ln \left( {1 + \frac{a}{{L + a}}} \right)\frac{{{\mu _0}{a^2}}}{{2\pi }}\\
\left| {{{\cal E}_3}} \right| = \frac{{d{\Phi _3}}}{{dt}} \sim \frac{{{\mu _0}}}{{2\pi }}\left( {ac\ln \left( {1 + \frac{a}{{L + a}}} \right) + ab\ln \left( {1 + \frac{a}{L}} \right)} \right)
\end{array}\]$$ $$\[\begin{array}{l}
\left| {{{\cal E}_1}} \right| = \frac{{d{\Phi _1}}}{{dt}} \sim \ln \left( {1 + \frac{a}{L}} \right)\frac{{{\mu _0}{a^2}}}{{2\pi }},\left| {{{\cal E}_2}} \right| = \frac{{d{\Phi _2}}}{{dt}} \sim \ln \left( {1 + \frac{a}{{L + a}}} \right)\frac{{{\mu _0}{a^2}}}{{2\pi }}\\
\left| {{{\cal E}_3}} \right| = \frac{{d{\Phi _3}}}{{dt}} \sim \frac{{{\mu _0}}}{{2\pi }}\left( {ac\ln \left( {1 + \frac{a}{{L + a}}} \right) + ab\ln \left( {1 + \frac{a}{L}} \right)} \right)
\end{array}\]$$](https://dxdy-04.korotkov.co.uk/f/f/8/5/f855e7a21fdc603973a98ac02b63b7cf82.png)
При этом, очевидно, для сопротивлений контуров можно выписать:
![$$\[{R_1} = {R_2} \sim 4a,{R_3} \sim 4a + 2b + 2c\]$$ $$\[{R_1} = {R_2} \sim 4a,{R_3} \sim 4a + 2b + 2c\]$$](https://dxdy-03.korotkov.co.uk/f/e/c/6/ec6d03907cde399278821f21ac40e01582.png)
Заметим, что их предыдущих равенств следует, что
![$$\[\frac{{{I_2}}}{{{I_1}}} = \frac{{\left| {{{\cal E}_2}} \right|}}{{\left| {{{\cal E}_1}} \right|}} = \frac{{\ln \left( {1 + \frac{a}{{L + a}}} \right)}}{{\ln \left( {1 + \frac{a}{L}} \right)}}\]$$ $$\[\frac{{{I_2}}}{{{I_1}}} = \frac{{\left| {{{\cal E}_2}} \right|}}{{\left| {{{\cal E}_1}} \right|}} = \frac{{\ln \left( {1 + \frac{a}{{L + a}}} \right)}}{{\ln \left( {1 + \frac{a}{L}} \right)}}\]$$](https://dxdy-01.korotkov.co.uk/f/8/6/2/8629f3252f6d7d6571453174a3a3265082.png)
Аналогично запишем:
![$$\[\frac{{\left| {{{\cal E}_3}} \right|}}{{\left| {{{\cal E}_2}} \right|}} = \frac{{ac\ln \left( {1 + \frac{a}{{L + a}}} \right) + ab\ln \left( {1 + \frac{a}{L}} \right)}}{{{a^2}\ln \left( {1 + \frac{a}{{L + a}}} \right)}} = \frac{c}{a} + \frac{b}{a} \cdot \frac{{{I_1}}}{{{I_2}}} = \frac{1}{a}\left( {c + b\frac{{{I_1}}}{{{I_2}}}} \right)\]$$ $$\[\frac{{\left| {{{\cal E}_3}} \right|}}{{\left| {{{\cal E}_2}} \right|}} = \frac{{ac\ln \left( {1 + \frac{a}{{L + a}}} \right) + ab\ln \left( {1 + \frac{a}{L}} \right)}}{{{a^2}\ln \left( {1 + \frac{a}{{L + a}}} \right)}} = \frac{c}{a} + \frac{b}{a} \cdot \frac{{{I_1}}}{{{I_2}}} = \frac{1}{a}\left( {c + b\frac{{{I_1}}}{{{I_2}}}} \right)\]$$](https://dxdy-03.korotkov.co.uk/f/6/5/9/65965d21518f3ca20293a41283c9072882.png)
С другой стороны
![$$\[\frac{{\left| {{{\cal E}_3}} \right|}}{{\left| {{{\cal E}_2}} \right|}} = \frac{{{I_3}{R_3}}}{{{I_2}{R_2}}} = \frac{{2a + b + C}}{{2a}}\frac{{{I_3}}}{{{I_2}}}\]$$ $$\[\frac{{\left| {{{\cal E}_3}} \right|}}{{\left| {{{\cal E}_2}} \right|}} = \frac{{{I_3}{R_3}}}{{{I_2}{R_2}}} = \frac{{2a + b + C}}{{2a}}\frac{{{I_3}}}{{{I_2}}}\]$$](https://dxdy-02.korotkov.co.uk/f/5/3/a/53a9ac08a951921e1bb554ff0964aa6a82.png)
откуда
![$$\[\frac{{2a + b + C}}{{2a}}\frac{{{I_3}}}{{{I_2}}} = \frac{1}{a}\left( {c + b\frac{{{I_1}}}{{{I_2}}}} \right) \Leftrightarrow {I_3} = \frac{{2\left( {b{I_1} + c{I_2}} \right)}}{{2a + b + C}}\]$$ $$\[\frac{{2a + b + C}}{{2a}}\frac{{{I_3}}}{{{I_2}}} = \frac{1}{a}\left( {c + b\frac{{{I_1}}}{{{I_2}}}} \right) \Leftrightarrow {I_3} = \frac{{2\left( {b{I_1} + c{I_2}} \right)}}{{2a + b + C}}\]$$](https://dxdy-04.korotkov.co.uk/f/f/f/5/ff55bfb7859ba691d91da1cc1c49c32082.png)
В ответе к задаче почему то написано
![$\[\frac{{2\left( {b{I_1} - c{I_2}} \right)}}{{2a + b + C}}\]$ $\[\frac{{2\left( {b{I_1} - c{I_2}} \right)}}{{2a + b + C}}\]$](https://dxdy-04.korotkov.co.uk/f/b/f/2/bf2bcfc8826426372164044133ab036582.png)
, как будто потоки

,

друг из друга вычитаются. В чем подвох?