Задача звучит так:
Покажите, что если функция

имеет в точке

все производные до порядка

включительно и
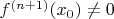
, то в остаточном члене формулы Тейлора, записанном в форме Лагранжа

,
где
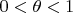
, величина

стремится к

при

Мне кажется, что задача сформулирована неправильно.
Во-первых потому, что производные определены только для точки

, а при

необходимо, чтобы производные высших порядков были определены в некоторой окрестности

. Соответственно вопрос: в какой?
Во-вторых, потому, что остаточный член по форме Лагранжа определяется так:

. Соответственно вопрос: что нужно изменить в изначальном равенстве -

на

или просто все

в правой части равенства заменить на

Прошу подсказать, как исправить задачу так, чтобы она имела смысл и резон решать её.