Решил нарисовать границу области принятия решения, исходя из следующих условий: внутри области лиса отслеживает координату

утки, на границе лисе должно быть одинаково бежать против часовой стрелки до северной точки встречи и до западной точки встречи, утка в обе точки встречи плывёт по горизонтальной или вертикальной прямой. Кривую рисовал лишь для области выше диагонали квадрата (т.е. 1/8 всей кривой), остальные части очевидно симметричны. Уравнение кривой (неявное):

, упрощать лень, так хоть видны явно оба пути лисы. Вот что получилось (область от центра до красных кривых), более вертикальную часть добавил исходя из симметрии:
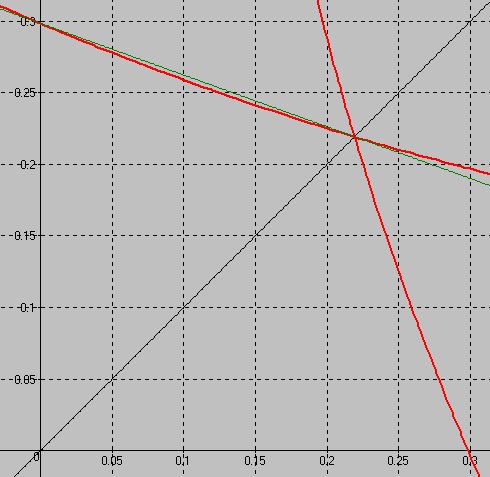
Серая кривая - диагональ квадрата, зеленая - прямая из северной точки границы в точку на диагонали (её наклон равен

, что сильно больше

). Координаты точек:

и

.
На самом деле есть сомнения в верности всех точек кроме на осях координат и пожалуй на диагонали. Потому что отсутствует условие возврата лисы к отслеживанию координат утки. Если же его добавить, то вопрос каково оно.
grizzly можете хотя бы словами его сформулировать? Какие пути лисы должны стать равными? Или где должна находиться утка после смены лисой стороны квадрата? Или лиса после старта обязательно (всегда, без всяких условий) добегает до угла и меняет сторону и лишь после этого может вернуться к отслеживанию координат утки если та внутри области принятия решения? Или даже не до угла, а до координаты

утки и лишь потом если утка внутри области то начинает отслеживать её координату, если снаружи - то продолжает бежать (в ту же сторону, условие разворота очевидно не выполняется)? В последнем случае кажется вся кривая становится верной ...