Вижу в научной статье, что две величины коррелируют между собой, по данным разных исследований, с коэффициентами корреляции от
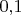
до

. Хочу объяснить человеку в одной фразе, что зависимость вроде бы есть, но она слабенькая. Желательно хлёстким примером, вроде "примерно так коррелируют бузина в огороде и дядька в Киеве". Но не могу нагуглить таких примеров, потому что по запросам типа "низкая корреляция примеры" выдаются только учебные упражнения. Можно бы обойтись и фразой типа "результат определяется этим фактором только на

процентов", но боюсь наврать, там же нюансы.
Может, кто-нибудь подскажет эффектный пример или фразу, которая была бы одновременно а) понятной полному чайнику б) грешила против истины не больше уровня нормального научпопа?



