О решении одной системы двух эллиптических кривых.Она встречается в задаче о рациональной точке в квадрате, расстояния которой до вершин квадрата рациональны.
Рассмотрим систему двух эллиптических кривых.
![$\[
\left\{ \begin{array}{l}
t^2 = \left( {x + a} \right)^2 + \left( {y + b} \right)^2 \\
z^2 = \left( {x + c} \right)^2 + \left( {y + d} \right)^2 \\
\end{array} \right.
\]$ $\[
\left\{ \begin{array}{l}
t^2 = \left( {x + a} \right)^2 + \left( {y + b} \right)^2 \\
z^2 = \left( {x + c} \right)^2 + \left( {y + d} \right)^2 \\
\end{array} \right.
\]$](https://dxdy-03.korotkov.co.uk/f/6/d/6/6d6b5b53cb0833f79389b970c846692082.png)
где
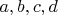
заданные рациональные числа.
Если вычесть из первого уравнения второе, а из полученного уравнения найти

и вставить его в первое уравнение, то придётся решать очень "тяжёлое" диофантовое уравнение от трёх переменных.
![$$\[
\left( {\frac{{t^2 - z^2 - 2\left( {b - d} \right)y - \left( {a^2 + b^2 - c^2 - d^2 } \right)}}{{2\left( {a - c} \right)}} + a} \right)^2 + \left( {y + b} \right)^2 = t^2
\]$ $$\[
\left( {\frac{{t^2 - z^2 - 2\left( {b - d} \right)y - \left( {a^2 + b^2 - c^2 - d^2 } \right)}}{{2\left( {a - c} \right)}} + a} \right)^2 + \left( {y + b} \right)^2 = t^2
\]$](https://dxdy-01.korotkov.co.uk/f/0/f/f/0ff50e2be000dbf57b609998d8a1436b82.png)
Здесь я покажу очень простой метод решения этой системы.
Для начала приведу необходимое для решения утверждение.
Если для рациональных чисел выполняется
![$\[a^2 + b^2 = c^2\]$ $\[a^2 + b^2 = c^2\]$](https://dxdy-02.korotkov.co.uk/f/1/1/9/1198df0126913e534485b2dc85548fb382.png)
, то существует единственное
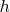
, что
![$$\[
a = c\frac{{1 - h^2 }}{{1 + h^2 }},b = c\frac{{2h}}{{1 + h^2 }}
\]$ $$\[
a = c\frac{{1 - h^2 }}{{1 + h^2 }},b = c\frac{{2h}}{{1 + h^2 }}
\]$](https://dxdy-01.korotkov.co.uk/f/4/3/a/43aa0f4015d35a42016d856fe13543b082.png)
и
![$$\[
a + bi = c\left( {\frac{{1 - h^2 }}{{1 + h^2 }} + \frac{{2h}}{{1 + h^2 }}i} \right)
\]$ $$\[
a + bi = c\left( {\frac{{1 - h^2 }}{{1 + h^2 }} + \frac{{2h}}{{1 + h^2 }}i} \right)
\]$](https://dxdy-02.korotkov.co.uk/f/d/c/a/dca25a7810f7a91b27b5b1e39027c76a82.png)
где

мнимая единица.
Напомню обозначения
![$$\[
C_h = \frac{{1 - h^2 }}{{1 + h^2 }},S_h = \frac{{2h}}{{1 + h^2 }}
\]$ $$\[
C_h = \frac{{1 - h^2 }}{{1 + h^2 }},S_h = \frac{{2h}}{{1 + h^2 }}
\]$](https://dxdy-01.korotkov.co.uk/f/0/5/3/05354fd07566bd2254cf54a4ca21d99e82.png)
Из начальных уравнений получим систему двух уравнений в комплексных числах
![$$\[
\left\{ \begin{array}{l}
\left( {x + a} \right) + \left( {y + b} \right)i = t\left( {C_m + S_m i} \right) \\
\left( {x + c} \right) + \left( {y + d} \right)i = z\left( {C_n + S_n i} \right) \\
\end{array} \right.
\]$ $$\[
\left\{ \begin{array}{l}
\left( {x + a} \right) + \left( {y + b} \right)i = t\left( {C_m + S_m i} \right) \\
\left( {x + c} \right) + \left( {y + d} \right)i = z\left( {C_n + S_n i} \right) \\
\end{array} \right.
\]$](https://dxdy-03.korotkov.co.uk/f/6/f/6/6f6debc0440bde07281f8d72c344722e82.png)
где
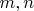
любые рациональные числа
Вычтем из первого уравнения второе
![$$\[
\left( {a - c} \right) + \left( {b - d} \right)i = \left( {tC_m - zC_n } \right) + \left( {tS_m - zS_n } \right)i
\]$ $$\[
\left( {a - c} \right) + \left( {b - d} \right)i = \left( {tC_m - zC_n } \right) + \left( {tS_m - zS_n } \right)i
\]$](https://dxdy-04.korotkov.co.uk/f/7/8/5/7857529d54e3a9b99e9c7fb6d489c7f182.png)
Приравняем мнимые и вещественные части
![$$\[
\left\{ \begin{array}{l}
tC_m - zC_n = a - c \\
tS_m - zS_n = b - d \\
\end{array} \right.
\]$ $$\[
\left\{ \begin{array}{l}
tC_m - zC_n = a - c \\
tS_m - zS_n = b - d \\
\end{array} \right.
\]$](https://dxdy-01.korotkov.co.uk/f/8/0/5/805bd3779c4afdb18d6bfedb32d4ea1782.png)
Отсюда находим
![$$\[
{t = \frac{{\left( {b - d} \right)C_n - \left( {a - c} \right)S_n }}{{S_m C_n - C_m S_n }},z = \frac{{\left( {b - d} \right)C_m - \left( {a - c} \right)S_m }}{{S_m C_n - C_m S_n }}}
\]$ $$\[
{t = \frac{{\left( {b - d} \right)C_n - \left( {a - c} \right)S_n }}{{S_m C_n - C_m S_n }},z = \frac{{\left( {b - d} \right)C_m - \left( {a - c} \right)S_m }}{{S_m C_n - C_m S_n }}}
\]$](https://dxdy-03.korotkov.co.uk/f/a/4/1/a41b251f5f20c96faf1af577c904432f82.png)
Подставив

в первое уравнение, и опять приравняв мнимые и вещественные, части находим

![$$\[
x = tC_m - a = \frac{{cC_m S_n - aS_m C_n + \left( {b - d} \right)C_m C_n }}{{S_m C_n - C_m S_n }}
\]$ $$\[
x = tC_m - a = \frac{{cC_m S_n - aS_m C_n + \left( {b - d} \right)C_m C_n }}{{S_m C_n - C_m S_n }}
\]$](https://dxdy-03.korotkov.co.uk/f/e/9/5/e952e6f2d04866f9b46c0e50a077d22582.png)
![$$\[
y = tS_m - b = \frac{{bC_m S_n - dS_m C_n - \left( {a - c} \right)S_m S_n }}{{S_m C_n - C_m S_n }}
\]$ $$\[
y = tS_m - b = \frac{{bC_m S_n - dS_m C_n - \left( {a - c} \right)S_m S_n }}{{S_m C_n - C_m S_n }}
\]$](https://dxdy-02.korotkov.co.uk/f/d/d/6/dd67f823d8555c74bde2c1b2db72786982.png)
Заменив введённые функции их значениями получим решение системы от двух переменных
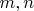
Приводить значения переменных

не буду из-за их громоздкости. Приведу код для PARI.
Код:
{
C_m=(1-m^2)/(1+m^2);
S_m=2*m/(1+m^2);
C_n=(1-n^2)/(1+n^2);
S_n=2*n/(1+n^2);
h=(S_m*C_n-C_m*S_n);
t=((b-d)*C_n-(a-c)*S_n)/h;
z=((b-d)*C_m-(a-c)*S_m)/h;
x=t*C_m-a;
y=t*S_m-b;
}
(x+a)^2+(y+b)^2-t^2
(x+c)^2+(y+d)^2-z^2