Клин из двоякопреломляющего вещества помещен на пути монохроматического света, поляризованного по кругу. Оптическая ось клина параллельна ребру клина. Свет, прошедший через клин, рассматривается через поляроид, главное направление которого составляет угол
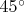
с ребром клина. Найти число темных полос

, наблюдаемых на поверхности клина. Максимальная толщина клина

см,

,

,

нм.
Моя попытка решения:
Свет поляризованный по кругу падает на клин, где разлагается на обычную и необыкновенную напряженность с разностью хода:

Затем он проходит на анализатор с углом поворота
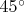
. Здесь у меня возникает сложность. Я не знаю угол поворота поляризатора который создал круговую поляризацию света.
Из-за этого я не могу выбрать из данных выражений внизу правильное.


Помогите разобраться.