Someoneок, понятно.
-- 03.06.2016, 13:36 --5. Уравнение

имеет в

единственное решение.
Доказательство.
Пусть

и

-- любые решения в

данного уравнения для некоторых

(не предполагаем, что они различные):

Добавим к обем сторонам каждого уравнения

:

Используем ассоциативность, коммутативность и аксиому 4 для левых сторон (на примере верхнего уравнения; с нижним все аналогично):

.
В итоге получим:

Отсюда следует, что

.
Следовательно, все решения данного уравнения равны друг другу, т.е. решение одно.
-- 03.06.2016, 13:39 --Меня смущает, что я в 5й задаче не использовал никакие из предыдущих результатов из этого листка. При желании конечно можно пойти немного другим путем, с использованием задачи 3, но я не уверен что так будет лучше и короче.
Добавим к каждому уравнению
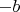
:

Используя коммутативность, ассоциативность и аксиому 4, получим:

Т.е.

и

являются противоположными элементами к

. Согласно зад.3, противоположный элемент единственен, значит

.
-- 03.06.2016, 14:23 --Совсем простая задачка.
6.

.
Доказательство.
Используем ассоциативность (аксиому 6):


 -- 03.06.2016, 14:31 --
-- 03.06.2016, 14:31 --Следующее доказательство очень похоже на доказательство задачи 2.
7. В

существует лишь одна единица.
Доказательство.
Пусть

и

-- две любые единицы из

. По аксиоме 7, для любого ненулевого

:

Взяв каждую из этих единиц в качестве

и используя коммутативность умножения, имеем

. Следовательно, все единицы равны другу другу, то есть единица одна.