Как он вообще пришел к такой вещи как группа? Я смутно понимаю даже что это.
Аксиомы группы появились не с бухты барахты.
Группы возникли вначале как группы преобразований.
Некоторое множество

отображений вида
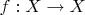
, где

- фиксированное множество, образует группу, если:
1) Композиция двух отображений из

принадлежит

(композиция - это значит, производим одно отображение, потом к результату сразу применяем второе);
2) Тождественное отображение (не меняющее ни одного элемента) принадлежит

;
3) Для каждого отображения из

обратное к нему принадлежит

.
(ассоциативность для композиции отображений выполняется автоматически)
Эти свойства присущи самым разным преобразованиям. Движения плоскости или пространства, повороты плоскости или пространства и т.д, аффинные преобразования (переводящие прямую сетку на плоскости например в скошенную под углом) и т.д. Некоммутативность здесь уже будет. Возьмите кубик Рубика. Если вы повернёте одну грань, а потом другую, то получится не то же самое, чем если вы повернёте сначала вторую, а потом первую, так же как в первом случае. Вот вам и некоммутативность. В группах преобразований некоммутативность - самое обычное дело.
Это уже потом выяснилось, что теми же свойствами обладают не только системы преобразований. И ввели аксиомы группы.
Совершенно каждое определение вводится не просто так и имеет ясный интуитивный смысл. Надо только его найти и понять. В этом есть интерес: в учебниках изложен сухой остаток, сухие формулировки и доказательства; надо стараться понять и представить, какие идеи стоят за этими формулировками.
-- 25.10.2015, 18:27 --Успешных в обычном смысле. Клубы, сауны, алкоголь...
Да зациклились вы на этом алкоголе и клубах! :) Вы явно завышаете значимость этой стороны жизни. Для очень многих людей, не только учёных, клубы - никакой не показатель. В жизни есть много более яркого и интересного, чем клубы и алкоголь.