Интересно, как обобщается формула интегрирования по частям на произвольные размерности.
(Ниже используются обозначения векторной алгебры в "физическом" варианте: вектор

скалярное произведение

векторное произведение
![$[\mathbf{ab}].$ $[\mathbf{ab}].$](https://dxdy-02.korotkov.co.uk/f/5/a/2/5a2ebb25764755cc5301c198b8aa5aeb82.png)
Также используются обозначения тензоров с индексами, обозначения дифформ. Если не оговорено, что формула касается дифформ,

имеет символический смысл элемента интегрирования. Если

- ориентируемое многообразие с краем, то

- его край с учётом ориентации, например: концы линии, линия края поверхности, поверхность 3-мерной области.)
Я однажды использовал нечто вроде:
![$$\int\limits_{S}[(\nabla f)\,\mathbf{v}]\,d\mathbf{S}=\oint\limits_{L=\partial S}f\,\mathbf{v}\,d\mathbf{L}-\int\limits_{S}f\,[\nabla\mathbf{v}]\,d\mathbf{S},$$ $$\int\limits_{S}[(\nabla f)\,\mathbf{v}]\,d\mathbf{S}=\oint\limits_{L=\partial S}f\,\mathbf{v}\,d\mathbf{L}-\int\limits_{S}f\,[\nabla\mathbf{v}]\,d\mathbf{S},$$](https://dxdy-01.korotkov.co.uk/f/c/7/6/c76546c86af14a591757dc7b5a31735282.png)
где

и

- скалярная и векторная функции,

- поверхность в трёхмерном пространстве,

нормален
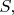
а

касателен к

но совершенно без обоснования. (Чтобы написать эту формулу, написал её частный случай в координатах, и "обобщил".)
Википедия даёт только такой частный случай:
Этого совершенно недостаточно. Хотелось бы общую формулу для многообразия в

и/или просто многообразия. В левой части подразумевается что-то вроде

в случае подмногообразия

или

в случае гладкого многообразия.