Граждане, помогите плз. с таким вопросом
Есть круг c центром

, на окружности которого отмечены точки

,

,

,

и

Радиусы к точкам

,

,

,

образуют два сектора. Первый сектор
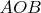
ограничен радиусами

и

, второй сектор

- радиусами

и

. Нужно найти площадь наложения этих секторов друг на друга.
Известны углы радиусов

,

,

,

относительно радиуса

- его принимаем за систему отсчета,

.
Секторы могут накладываться друг на друга, могут не накладываться. Точки

,

,

,

могут быть расположены на окружности в любом порядке.
Если

и

, то всё считается - берем

- дальше по формуле площади сектора.
Но вот что делать, если

, а

? т.е. сектор повернут как бы "через

" (радиус

оказывается внутри одного или двух секторов)? По идее, надо как-то повернуть оба сектора на некоторый угол, чтобы возникла ситуация, когда они не проходят "через

". На какой именно угол нужно повернуть?
Вообще, насколько понимаю, возможны следующие разновидности наложений секторов:
- Если оба сектора не проходят через
 , то это можно описать как
, то это можно описать как
- сектора не накладываются друг на друга.
- сектора накладываются друг на друга одним участком (тогда считаем угол сектора наложения по формуле, приведенной выше).
- Если один или оба сектора проходят через
 , то тут уже такие варианты:
, то тут уже такие варианты:
- сектора не накладываются друг на друга.
- сектора накладываются друг на друга одним участком
- сектора накладываются двумя участками (например,
 )
)
В общем, голову поломал уже, плиз хелп.